1. Introduction
Large pre-trained 언어모델에 대해서 8-bit quantization을 적용하는 기법들이 많이 연구되었지만, 이런 기법들은 350M 이하 스케일에 대해서만 연구되는 경우가 많았습니다. 이 논문에서는 performance 감소없이 billion 단위에서도 적용 가능한 quantization 기법을 제시합니다.
이 논문에서는 파라미터 스케일이 6B정도가 되었을 때 Transformer에만 나타나는 특이한 현상이 있다고 합니다. 트랜스포머 레이어 전체에서 25% 정도에서만 관찰이 된다고 하는데, 특정 차원의 feature 크기가 다른 차원의 feature 크기보다 20배정도 크게 나타난다고 합니다.
Transformer에서만 관측되는 특이한 현상을 분석하기 위해서 논문에서는 13B parameter를 가진 모델에 대해서 feature 차원의 크기를 비교했고, 값이 6보다 큰 feature를 outlier로 간주했습니다. 그리고 실험을 할 때 특정 library에 있는 오류로 인한 영향을 없애기 위해서 3개의 software(OpenAI, Fairseq, EleutherAI)에 구현된 GPT-2 model을 모두 사용해서 실험을 진행했습니다.
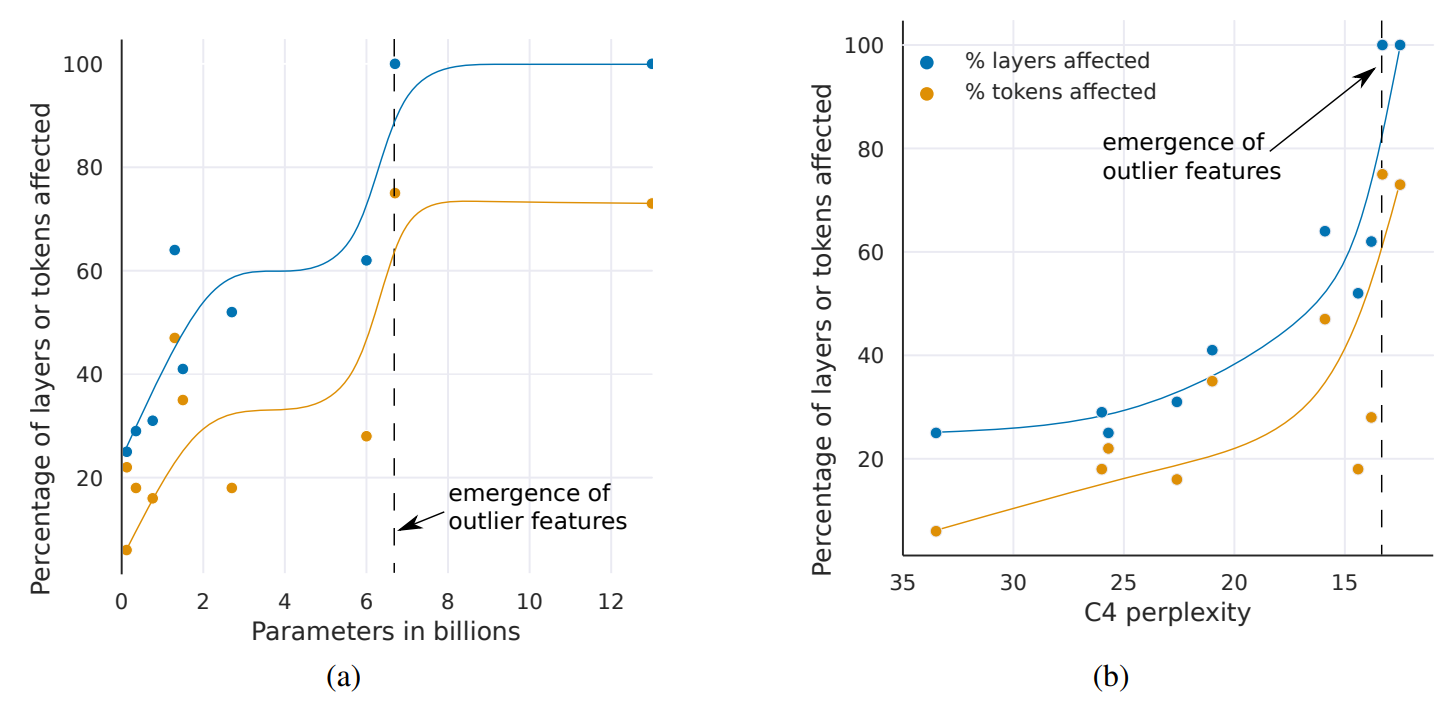
위의 그림 (a)는 모델 파라미터 수를 늘림에따라 outlier로 인해 영향을 받는 sequence의 비율을 측정한 것입니다. 예를들어 sequence의 i번째 단어에 특정 차원에 outlier가 등장했는데, 해당 outlier가 다른 단어에 얼마나 영향을 끼치는지를 측정한 값입니다. 그림을 보면 파라미터 수가 6B에서 6.5B로 넘어갈 때 영향을 받는 비율이 급격히 증가한다는 것을 볼 수 있습니다.
위에 그림 (a)에서는 perplexity가 감소할수록 outlier feature의 median magnitude값이 커지는 것을 관찰할 수 있는데, 이로 인해 transformer에 Int8 quantization을 적용했을 때 성능이 좋지 않습니다. 왜냐하면 특정 feature의 값이 커지면 quantization range가 커져서 대부분 quantization bin은 비어있는 상태가 되고, 원래 값이 작았던 feature는 0에 가까운 값으로 quantization이 진행되기 때문에 정보 손실이 많이 발생하게 됩니다. 또한 Int8 quantization 뿐만 아니라 16-bit quantization 방법도 마찬가지로 6.7B scale을 넘어가면 outlier로 인해 잘 작동하지 않을 것이라고 논문에서 주장합니다.
또한 그림(b)에서는 perplexity가 감소함에 따라 outlier feature 개수가 증가하는 것을 볼 수 있습니다. 논문에서는 6.7B transformer에서 2,048 sequence 기준으로 150k 정도의 outlier feature를 관측했다고 하는, 이런 outlier들은 6개의 hidden dimension에 집중되어있다고 합니다.
이런 outlier는 transformer performance에 큰 영향을 끼치는데, 만약 이 7개의 차원을 제거하면 top-1 softmax probability값이 40%에서 20%로 줄어들고, vadliation perplexity 값이 600~1,000% 증가한다고 합니다. 만약에 임의의 7개의 차원을 제거한다면 top-1 probability는 0.02~0.3% 만큼 감소하고 perplexity는 0.1%만큼 증가한다고 하는데, 이런 실험은 outlier feature가 성능에 얼마나 중요한 역할을 하는지 나타냅니다. 그래서 이런 outlier feature들에 대해서 좀 더 quantization precision을 높이면 large scale transformer에서도 모델의 성능을 유지한 채 quantization 기법을 적용할 수 있게 될거라고 논문에서 주장하고 있습니다.
이 논문에서 제시한 기법은 앞서 관측된 outlier를 고려해서 quantization 기법을 수행하는 방법입니다. 방법을 요약하자면 outlier feature 차원에 대해서는 16-bit quantization 기법을 적용하고, 그 외의 차원에 대해서는 8-bit quantization을 적용하는 방법입니다.
2. Background
2.1. 8-Bit Data Types and Quantization
Absmax quantization은 입력을 8-bit 범위 \([-127,127]\)로 바꾸는 방법인데, 127을 곱하고 입력 tensor의 infinity norm으로 나눠주는 방식으로 다음과 같이 계산합니다. 여기서 \(\lfloor \rceil\)은 반올림을 나타냅니다.
\[\mathbf{X}_{i 8}=\left\lfloor\frac{127 \cdot \mathbf{X}_{f 16}}{\max _{i j}\left(\left|\mathbf{X}_{f 16_{i j} \mid}\right|\right)}\right\rfloor=\left\lfloor\frac{127}{\left\|\mathbf{X}_{f 16}\right\|_{\infty}} \mathbf{X}_{f 16}\right\rceil=\left\lfloor s_{x_{f 16}} \mathbf{X}_{f 16} \mid\right.\]Zeropoint quantization은 입력 분포를 normalized dynamic range \(nd_x\)만큼 scale한 후에 zeropoint \(zp_x\)만큼 이동시키는 방법입니다. 입력이 asymmetric distribution인 경우에, Absmax를 사용하면 일부 bit만 사용해서 quantization이 진행되는데, zeropoint 방법을 상요하면 전체 bit를 다 사용해서 입력데이터를 표현할 수 있습니다.
3. Int8 Matrix Multiplication at scale
단일 scaling constant로 quantization을 수행할 때 문제점은 tensor안에 outlier가 1개라도 존재하면 tensor안에 다른 값들의 quantization precision을 감소시킬 수 있기 때문입니다. 그래서 tensor를 여러 block으로 나누고 각 block마다 다르게 scailing factor를 계산하면 outlier의 영향을 block 안으로 한정시킬 수 있습니다. 이 논문에서는 tensor를 vector 단위로 나눠서 outlier의 영향을 줄였습니다.
3.1. Vector-wise Quantization
Hidden states \(\mathbf{X}_{f 16} \in \mathbb{R}^{b \times h}\)와 weight matrix \(\mathbf{W}_{f 16} \in \mathbb{R}^{h \times o}\)를 곱하는 상황에서, \(\mathbf{X}_{f 16}\)의 각 row에 다른 scale constant \(c_{x_{f 16}}\)를 할당하고, \(\mathbf{W}_{f 16}\)의 각 column에 다른 scale constant \(\mathbf{c}_{w_{f 16}}\)를 할당해서 quantization을 수행하면, dequantize를 할 때 \(c_{x_{f 16}}\)와 \(\mathbf{c}_{w_{f 16}}\)의 outer product를 이용할 수 있습니다. 그래서 Vector-wise quantization을 통해 Int8 matrix multiplication을 수행하는 과정을 다음과 같이 나타낼 수 있습니다.
\[\mathbf{X}_{f 16} \mathbf{W}_{f 16}=\mathbf{C}_{f 16} \approx \frac{1}{\mathbf{c}_{x_{f 16}} \otimes \mathbf{c}_{w_{f 16}}} \mathbf{C}_{i 32}=S \cdot \mathbf{C}_{i 32}=\mathbf{S} \cdot \mathbf{A}_{i 8} \mathbf{B}_{i 8}=\mathbf{S} \cdot Q\left(\mathbf{A}_{f 16}\right) Q\left(\mathbf{B}_{f 16}\right)\]16-bit floating point precision을 가진 두 행렬 \(A, B\)를 곱할 때, 앞서 말한 vector-wise scale factor를 통해 quantization을 수행해서 int8로 변환하고, 변환한 행렬을 곱하고 다시 scale factor의 outer product로 나눠주면 원래 float 16으로 행렬곱 한 것을 근사하게 됩니다.
3.2. The core of LLM.int8(): Mixed-precision Decomposition
위에서 large scale transformer의 outlier를 분석한 결과에 따르면, outlier는 특정 feature 차원에 집중되어 있기 때문에 outlier가 없는 차원에만 quantization을 하면 성능을 유지한 채 quantization 기법을 적용할 수 있다고 합니다.
그래서 feature 차원 중에서 값이 6.0 이상인 feature의 차원을 \(O=\{i \mid i \in \mathbb{Z}, 0 \leq i \leq h\}\)에 집어넣고, 이 집합에 속한 차원에 대해서는 float 16 행렬곱을 수행하고, 나머지 차원에 대해서는 int8 vector-wise quantization을 적용해서 행렬곱을 수행합니다.
\[\mathbf{C}_{f 16} \approx \sum_{h \in O} \mathbf{X}_{f 16}^h \mathbf{W}_{f 16}^h+\mathbf{S}_{f 16} \cdot \sum_{h \notin O} \mathbf{X}_{i 8}^h \mathbf{W}_{i 8}^h\]이런 방식이 효과적인 이유는 outlier 차원의 비율이 0.1% 정도이기 때문에, 나머지 99.9%의 차원에 대해서는 메모리 측면에서 효율적인 8-bit 행렬곱을 할 수 있기 떄문입니다.
4. Experiment
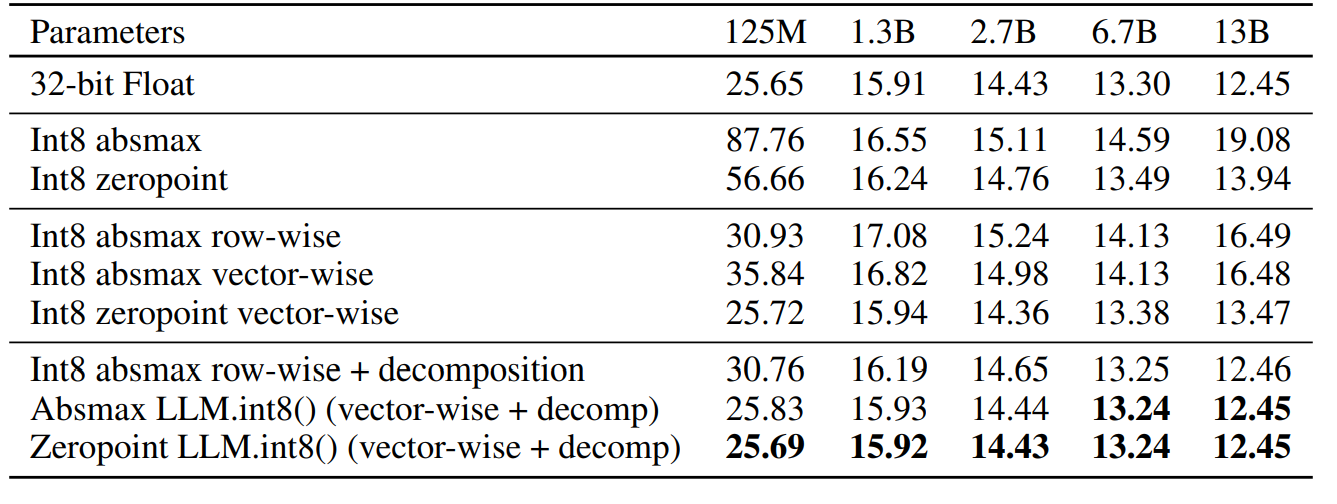
이 논문에서는 2개의 실험을 했는데 large scale transformer에 대해서 language modeling 성능과 zero shot accuracy 성능을 기존의 quantization 기법과 비교했습니다. 먼저 Language Modeling 성능은 파라미터 수를 점점 증가시킴에 따라 perplexity 값을 기존의 quantization 기법과 비교를 하는 방식으로 진행했습니다. 데이터는 C4 corpus validation data를 사용했습니다.
실험 결과를 보면 다른 quantization 기법들은 6.7B scale 이후에 fp32와 비교해서 perplexity 값이 커졌다는 결과가 나타나는데, 논문에서 제시한 방법은 fp32와 비교해서도 perplexity 값이 거의 차이가 나지 않는 결과가 나타났습니다.
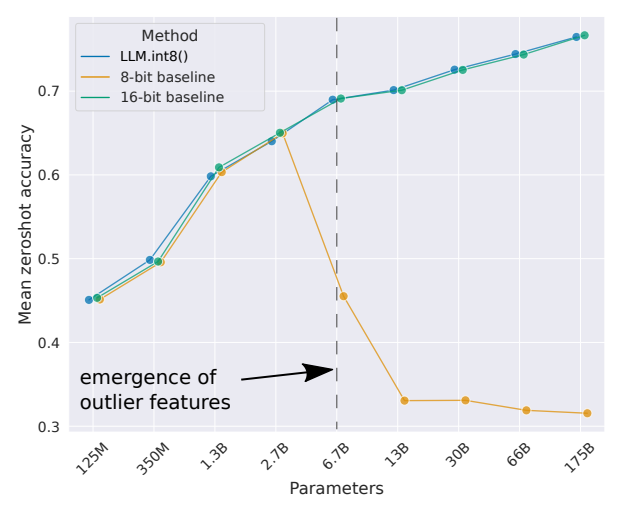
그 다음에 OPT model을 사용해서 zero shot accuracy 성능을 비교했는데, 그림을 보면 스케일이 2.7B보다 작을 때는 기존의 8-bit quantization 기법과 논문에서 제시한 기법이 성능이 비슷하지만, 6.7B 정도 스케일이 되었을 때는 성능 차이가 많이 나는 결과가 나타났습니다.
5. Discussion and Limitations
이 논문에서는 transfomer의 특징을 분석해서 multi-billion scale에 대해서도 잘 작동하는 Int8 quantization 기법을 제시했습니다. 이 방법의 한계는 Int8 data type에만 적용이 가능하단 점인데, Int8로 굳이 한 이유는 현재 GPU와 TPU가 8-bit 중에서 int type만 지원하기 때문입니다. 현재 GPU와 TPU가 8-bit floating point를 지원하지 않기 때문에, 이 방법은 연구하지 않았다고 합니다.
또한 스케일이 175B 까지만 한정되어 있는데, 그 이상 모델이 커지면 다른 추가적인 특성 때문에 논문에서 제시한 quantization 기법이 잘 적용되지 않을 수도 있다고 합니다. 마지막으로 논문에서 제시한 기법은 attention function에는 적용하지 않았는데, 그 이유가 attention function에는 parameter가 포함되지 않아서 quantization을 적용해도 메모리 사용량 감소가 일어나지 않기 때문이라고 합니다.

Comments powered by Disqus.