1. Introduction
Momentum이나 Adam optimizer는 시간에 따른 gradient 통계량 정보를 이용해서 다음 그레디언트를 업데이트할 때 그레디언트의 방향을 조절하거나 학습률을 조절합니다. 이런 방식은 일반적인 SGD optimizer에 비해서 학습을 가속화 시켜준다는 장점이 있지만, gradient 통계량 정보를 계속 가지고 있어야 하기 때문에 SGD를 사용할 때 보다 더 큰 메모리가 필요하게 됩니다.
\[\begin{gathered} \\\\ \text { Momentum }\left(\mathbf{g}_t, \mathbf{w}_{t-1}, \mathbf{m}_{t-1}\right)= \begin{cases}\mathbf{m}_0=\mathbf{g}_0 & \text { Initialization } \\ \mathbf{m}_t=\beta_1 \mathbf{m}_{t-1}+\mathbf{g}_t & \text { State 1 update } \\ \mathbf{w}_t=\mathbf{w}_{t-1}-\alpha \cdot \mathbf{m}_t & \text { Weight update }\end{cases} \\\\\\ \text { Adam }\left(\mathbf{g}_t, \mathbf{w}_{t-1}, \mathbf{m}_{t-1}, \mathbf{r}_{t-1}\right)= \begin{cases}\mathbf{r}_0=\mathbf{m}_0=\mathbf{0} & \text { Initialization } \\ \mathbf{m}_t=\beta_1 \mathbf{m}_{t-1}+\left(1-\beta_1\right) \mathbf{g}_t & \text { State 1 update } \\ \mathbf{r}_t=\beta_2 \mathbf{r}_{t-1}+\left(1-\beta_2\right) \mathbf{g}_t^2 & \text { State 2 update } \\ \mathbf{w}_t=\mathbf{w}_{t-1}-\alpha \cdot \frac{\mathbf{m}_t}{\sqrt{\mathbf{r}_t}+\epsilon} & \text { Weight update, }\end{cases}\\\\ \end{gathered}\]위에 식은 Momentum과 Adam을 사용할 때 state 정보를 사용해서 gradient를 업데이트 하는 과정입니다. 만약에 32 bit로 state를 저장하게 된다면, Momentum은 파라미터 1개 당 4 bytes Adam은 8 bytes가 추가적으로 필요하게 됩니다. 만약에 파라미터 수가 1B정도 된다면 각각 4GB, 8GB만큼 메모리가 추가적으로 필요합니다.
실제로 optimi-zer state는 학습 과정에서 대략 전체 메모리의 33%~75% 정도를 차지한다고 합니다. Largest GPT-2에 대한 optimizer state는 약 11GB, T5에 대한 state는 41GB 정도 된다고 하는데, 이 논문에서는 optimizer state를 8 bit로 저장하는 8-bit optimizer를 통해 학습 과정에서 메모리를 절약할 수 있는 방법을 제시했습니다.
이처럼 quantization을 통해 bit수를 줄여서 학습을 할 때는 크게 3가지 문제가 있습니다. 먼저 적은 bit를 사용했을 때 accuracy가 많이 차이가 나면 안되고 (quantization accuracy), quantization을 적용하는 속도가 빨라야하고 (computational efficiency), 커다란 모델에 대해서도 학습이 안정적으로 이루어져야 합니다 (large-scale stability).
이 논문에서는 위에 3가지 문제를 block-wise quantization을 통해 해결합니다. Block-wise quantization은 입력 tensor를 block으로 나누고, 각 block마다 quantization을 독립적으로 수행하는 방법입니다. 이렇게 block 단위로 나눠서 진행하는 이유는 모든 tensor에 대해 quantization을 수행하면 특정 outlier로 인해서 제대로 안되는 경향이 있는데, block 단위로 나누면 outlier가 block 안에만 한정되니까 학습 안정성과 성능이 증가한다는 장점이 있기 때문입니다.
Block-wise quantization 이외에도 dynamic quantizatino과 stable embedding layer 방법을 추가적으로 제시해서 8-bit optimizer의 안정성과 성능을 향상시켰습니다.
2. Background
2.1. Non-linear Quantization
Quantization은 precision을 희생하면서 numeric representation을 압축하는 방법입니다. 수식적으로는 \(k\)-bit 정수를 실수로 매핑시켜주는 과정인데, \(\mathbf{Q}^{\text {map }}:\left[0,2^k-1\right] \mapsto D\)으로 표현이 가능합니다. 예를들어 IEEE 32-bit floating point는 \(0 \ldots 2^{32}-1\)를 \([-3.4 \mathrm{e} 38,+3.4 \mathrm{e} 38]\) 으로 대응시킵니다. 일반적인 quantization은 다음과 같은 3단계를 거칩니다.
(1) 입력 tensor \(T\)가 주어졌을 때 표현 가능한 정수 영역으로 대응시키기 위해 normalization constant \(N\)으로 나눠줍니다.
(2) \(\frac{T}{N}\)과 가장 가까운 값 \(q_i\)을 \(D\)에서 찾습니다.
\[\mathbf{T}_i^Q=\underset{j=0}{\arg \min }\left|\mathbf{Q}_j^{\text {map }}-\frac{\mathbf{T}_i}{N}\right|\](3) \(q_i\)에 해당하는 index \(i\)를 따로 저장합니다.
이렇게 qunatization 과정을 거치고, dequantization을 수행할 때는 index를 mapping 함수에 집어넣고 \(N\)을 곱하는 형태로 수행됩니다.
\[\mathbf{T}_i^D=\mathbf{Q}^{\operatorname{map}}\left(\mathbf{T}_i^Q\right) \cdot N\]2.2. Dynamic Tree Quantization
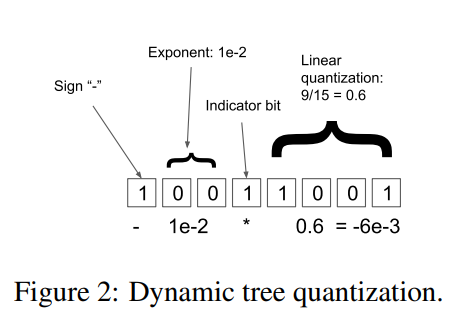
Dynamic quantization은 quantization을 적용하는 값의 크기가 클때나 작을 때 quantization error를 줄이는 기법입니다. 고정된 exponent, fraction을 사용하는 대신에 값에따라 exponent와 fraction을 변화시킵니다.
위의 그림 처럼 4개의 부분으로 나뉘는데, indicator bit를 통해 exponent와 fraction을 조절합니다. Indicator bit는 sign bit이후에 처음으로 1로 세팅되는 bit입니다. 일반적인 linear quantization 방법과 비교해서 quantization error가 낮다는 장점이 있지만, 대상이 되는 값의 범위가 \([-1.0,1.0]\)안에 있어야 해서 absolute max normalization 과정이 필요합니다.
3. Proposed Method
8-Bit optimizer는 block-wise quantization, dynamic quantization, stable embedding layer로 이루어져있습니다. 이 3개의 components를 통해 optimizer state를 8-bit로 저장하고, update를 수행할 때 state를 32-bit로 dequantize한 다음, 저장할 때 다시 8-bit로 quantization을 수행하는 과정으로 진행이 됩니다. 이 과정이 register 안에서 수행되도록 만들었기 때문에 GPU memory copy가 일어나지 않고 추가적으로 임시 메모리도 필요하지 않습니다.
3.1. Block-wise Quantization
Block-wise quantization을 통해 outlier를 특정 block에 한정시켜서 normalization 비용을 줄이고 quantization precision을 증가시켰습니다. Dynamic quantization을 수행하기 위해서 tensor의 범위를 \([-1, 1]\)로 맞춰줘야 하는데, 전체 tensor에 대해서 normalize를 한번에 진행하게 되면 core 사이에 synchronization 과정이 수반되기 때문에 속도가 느립니다. 하지만 Block 단위로 normalization을 진행하게 되면 synchronization 과정이 필요가 없어서 이 비용을 줄일 수 있습니다.
3.2. Dynamic Quantization
기존의 Dynamic tree quantization 방법을 확장해서 논문에서 제시한 방법을 dynamic quantization이라고 명명했는데, sign bit를 제거하고 fraction bit를 고정시킨 방법이라고 합니다. Sign bit를 없앤 이유는 Adam optimizer에서 second state가 strictly positive여서 필요하지 않기 때문이고, second Adam state의 magnitude가 3~5 order로 변하기 때문에 fraction bit를 고정시켰다고 합니다. 여기서 의문이 드는건 fraction bit를 고정시키면 더이상 dynamic 형태로 quantization 진행이 안되는거 아닌가? 생각이 들어 그 부분이 아직 이해가가지 않습니다.
3.3. Stable Embedding Layer
NLP에서 사용하는 일반적인 Embedding layer와 유사한데, 차이점은 초기화할 때 Xavier uniform 분포를 사용한다는 것과 position embedding을 추가하기 전에 layer normalization을 적용한다는 점입니다. Normal distribution으로 초기화하면 outlier로 인해서 gradient 크기가 커질 수 있기 때문에 학습이 불안정해지고, layer normalization을 통해 variacne를 작게 유지해서 학습의 안정성을 높였습니다.
3.4. Summary
지금까지 제시한 방법을 정리하면 위와 같습니다. 왼쪽 quantization 과정을 보면 Optimizer state를 block 단위로 나누고, block 안에서 absolute maximum 값을 통해 normalization을 수행합니다. 그 후에 Dynamic quantization을 통해 normalized value와 가장 가까운 8-bit value를 찾습니다. 그렇게 찾은 8-bit value에 대응하는 index를 저장하는 과정을 거칩니다. Dequantization 과정은 앞에서 구한 index를 이용해서 lookup table을 통해 8-bit value를 얻고, denomalization 과정을 거쳐 원래 값을 복원합니다.
4. 8-Bit vs 32-Bit Optimizer performance for Benchmarks
4.1. Experimental Setup
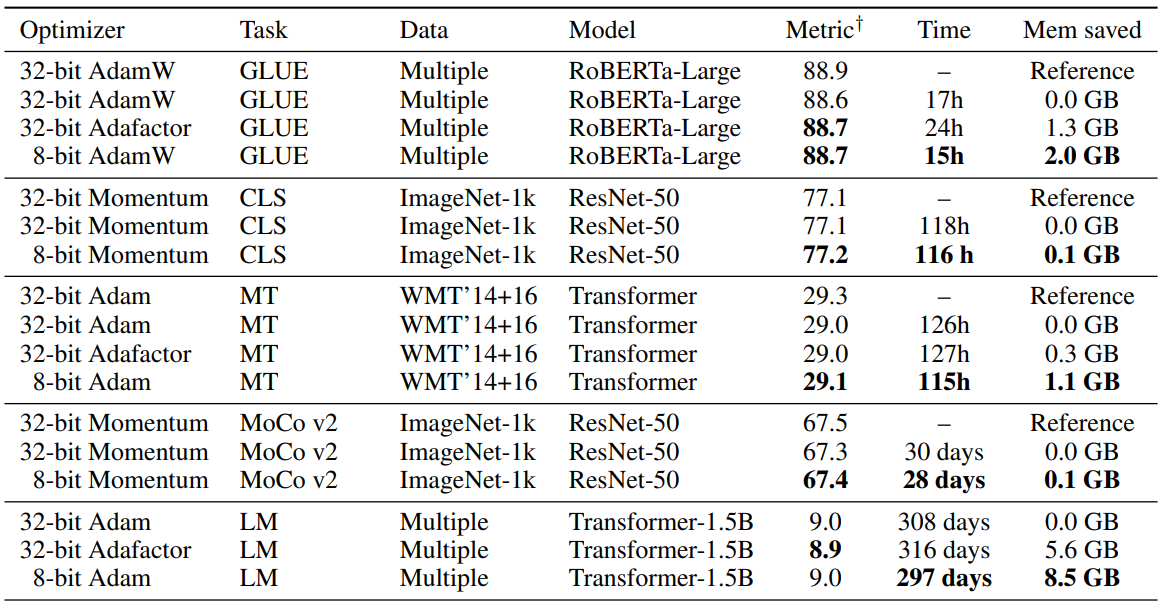
실험에서는 Adam, AdamW, Momentum을 기준으로 비교를 했고, 하이퍼파라미터나 weight, gradient, activation의 precision을 변경하지 않은 채 Adam, AdamW, Momentum을 기준으로 비교를 했습니다.
위에 표는 여러 task에서 8-bit optimizer를 사용했을 때 성능이 변하지 않은 채 학습 시간과 모델 크기가 줄어들었다는 것을 보여주는 실험결과입니다. Momentum을 기준으로는 변화가 크지 않지만, Adam을 기준으로 비교했을 때는 학습시간과 필요한 메모리 크기가 꽤 많이 줄어들었다는 것을 볼 수 있습니다.
4.2. Ablation Analysis
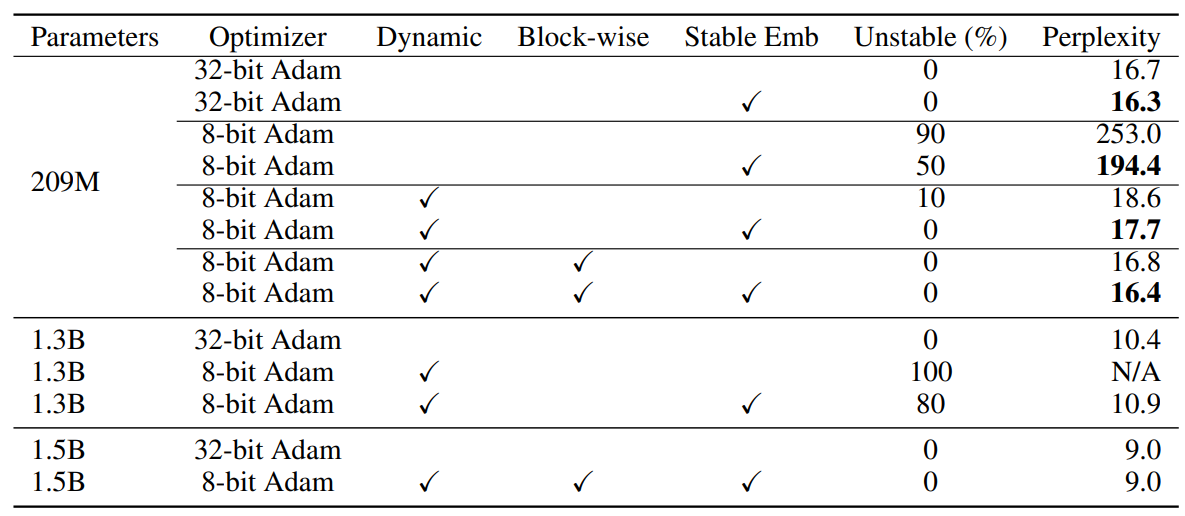
작은 언어모델과 큰 언어모델의 perplexity와 학습 안정성을 기준으로 ablation study를 진행했습니다. Stability는 하이퍼 파라미터를 다르게 바꾸면서 학습했을 때 모델의 성능이 어느정도 되는지를 기준으로 측정했습니다. 표를 보시면 작은 스케일 모델에서는 Dynamic quantization, block-wise quantization 영향은 거의 없고, stable embedding을 사용했을 떄 학습 안정성이 증가했습니다. 큰 스케일 모델에서는 Dynamic quantization, Block-wise quantization 영향이 중요하다는 걸 보여주고 있습니다.
5. Discussion & Limitations
8-bit optimizer는 다양한 task에서 memory 사용량을 낮추고 학습 과정을 가속시키지만, 모델 파라미터에 비례해서 메모리 사용량을 줄이기 때문에 CNN처럼 activation memory를 많이 차지하는 모델에서는 적용하기 어렵습니다. 또한 8-bit optimizer를 NLP에 적용하기 위해서는 논문에서 제시한 stable embedding layer가 필요하다는 단점이 있습니다.

Comments powered by Disqus.