A Comprehensive Survey on Graph Neural Networks 정리

1. Introduction

딥러닝은 Euclidean space에서 표현된 데이터에 대해서 성공적인 성과를 거두었지만, 최근에 non-Euclidean space에서 생성된 데이터에 딥러닝을 적용하려는 시도가 많아지고 있습니다. 본 논문에서는 GNN을 4개의 카테고리 (Recurrent GNN, Convolutional GNN, Graph autoencoder, Spatial-temporal GNN)으로 나누어서 소개하고 있습니다.

2. Categorization and Frameworks

먼저 GNN의 taxonomy와 framework에 대해서 간단하게 소개하고, 각각의 요소들을 나중에 자세히 다루겠습니다.

2.1. Taxonomy

Recurrent graph neural networks (RecGNNs)의 목표는 recurrent neural architecture를 사용해서 node representation을 학습하는 것입니다. RecGNNs에서는 각 노드가 안정상태가 될때까지 주위에 이웃 노드와 정보를 계속 교한한다는 가정을 합니다. RecGNNs는 개념적으로 중요하고 이후에 많은 연구에 영향을 주었는데, 특히 메시지 패싱 아이디어는 spatial-based convolutional GNN에서 사용됩니다.

Convolutional graph neural networks (ConvGNNs)는 convolution 연산을 grid 에서 graph data로 확장했습니다. RecGNNs와 차이점은 ConvGNNs는graph convolutional layer를 여러개 쌓아서 고차원 노드 representation을 추출한다는 점입니다.

Graph autoencoders (GAEs)는 node 혹은 graph를 latent space로 인코딩하는 프레임워크입니다. GAEs는 네트워크 임베딩이나 graph generative distribution을 만들 때 사용합니다.

Spatial-temporal graph neural networks (STGNNs)는 spatial-temporal graph에서 숨겨진 정보를 학습하는 걸 목표로 합니다. STGNNs의 주요 아이디어는 spatial dependency와 temporal dependency를 동시에 고려한다는 점입니다. 현재 대부분 접근 방법들은 graph convolution을 통해 spatial 정보를 반영하고, RNN이나 CNN을 통해 temporal 정보를 반영하는 방식입니다.

2.2. Frameworks

Graph 구조와 노드에 포함된 정보가 입력으로 주어졌을 때, GNN의 출력값은 graph analytic task에 따라 달라집니다.

Node-level의 출력값은 node regression이나 node classification과 관련이 있습다. RecGNN와 ConvGNN이 information propagation 혹은 graph convolution을 사용해서 고차원 node representation을 추출한 후에, multi-perceptron 혹은 softmax layer를 사용해서 node-level task를 수행합니다.

Edge-level의 출력값은 edge classification 혹은 link prediction task와 관련이 있습니다. 두 개의 노드의 hidden representation을 입력으로 받고, 유사도 함수나 뉴럴 네트워크를 통해 edge의 레이블이나 연결 강도를 예측하는 테스크를 해결합니다.

Graph-level의 출력값은 graph classification task와 연관이 있습니다. Graph 단위로 compact representation을 얻기 위해서 GNN은 종종 pooling 혹은 readout 연산과 결합이 됩니다.

2.3. Training Frameworks

많은 GNN은 (semi-) supervised 혹은 unsupervised 방식으로 학습이 가능합니다.

• Semi-supervised learning for node-level classification

일부 노드가 label 되고 나머지 노드가 label 되지 않았을 때, ConvGNN은 학습을 통해 unlabeled node에 대해서 label을 할당할 수 있습니다.

• Supervised learning for graph-level classification

그래프 수준의 분류는 전체 그래프에 대해서 class label을 예측하는 것을 목표로 합니다. 이 태스크에서 모델의 구조는 graph convolutional layer, graph pooling layer, readout layer로 이루어집니다. Graph convolutional layer에서는 고차원 node representation을 추출하고, graph pooling layer에서는 down sample을 수행해서 graph 구조를 coarse하게 변형합니다. 이후에 readout layer에서 node representation을 합쳐서 graph representation으로 만들고, multi-layer perceptron 혹은 softmax layer를 사용해서 그래프 레이블을 예측합니다.

• Unsupervised learning for graph embedding

Graph에서 이용가능한 class label이 없을 때, unsupervised 방식으로 graph embedding을 할 수 있습니다. 두 가지 방식으로 수행이 가능한데, 첫째는 graph convolutional layer를 사용해서 graph를 인코딩하고, 디코더를 사용해서 graph를 복원하는 방법입니다. 두번째 방법은 negative sampling을 사용해서 negative node pair를 생성하고, 그래프에 있는 node pair를 positive로 삼는 방법입니다. 후에 regression layer를 사용해서 positive와 negative pair를 구분합니다. 이제 하나씩 자세히 살펴보겠습니다.

3. Recurrent Graph Neural Networks

RecGNN은 GNN의 선구자입니다. 같은 파라미터 집합을 그래프의 전체 노드에 반복적으로 적용해서 고차원 노드 정보를 추출합니다. 계산량이 많아서 초기 연구들은 directed acyclic graphs (DAG)에만 적용이 되었습니다.

이전에 DAG에 대해서만 다룬 GNN을 Scarselli가 acyclic, cyclic, directed, undirected graph로 확장해서 적용했습니다. Information diffusion mechanism을 기반으로, GNN은 안정 상태에 도달하기 전까지 이웃 노드와 정보를 교환하면서 노드의 정보를 다음과 같이 업데이트합니다.

\[\mathbf{h}_v^{(t)}=\sum_{u \in N(v)} f\left(\mathbf{x}_v, \mathbf{x}_{(v, u)}^{\mathbf{e}}, \mathbf{x}_u, \mathbf{h}_u^{(t-1)}\right)\]

현재 시점 노드 ($v$)와 이웃 노드 ($u$), edge, 이전시점 (t-1)의 이웃 노드 hidden state를 사용해서 현재 시점의 노드의 hidden state를 업데이트합니다. $\mathbf{h}_v^{(0)}$ 는 처음에 임의로 초기화되고 $f$는 parametric 함수입니다. 수렴성을 보장하기 위해서, $f$는 반드시 contraction mapping 이어야 합니다. contraction mapping이란 latent space로 projection한 후에 두 점 사이의 거리가 줄어든다는 것을 의미합니다. $f$가 만약 뉴럴네트워크라면 Jacobian matrix를 통해 파라미터에 penalty term을 추가합니다. GNN이 반복적으로 node state를 전파하고 loss function에 대한 파라미터 gradient를 계산하다가, 수렴 조건이 만족되면 마지막 hidden state가 readout layer를 통과합니다.

Gated Graph Neural Network (GGNN)은 gated recurrent unit (GRU)를 recurrent function으로 이용해서 반복횟수를 줄였습니다. 이 방법의 장점은 수렴성을 보장하기 위해 파라미터에 제약을 걸 필요가 없다는 점입니다. 업데이트는 다음과 같이 진행됩니다.

\[\mathbf{h}_v^{(t)}=G R U\left(\mathbf{h}_v^{(t-1)}, \sum_{u \in N(v)} \mathbf{W h}_u^{(t-1)}\right)\]

이전 시점 (t-1)의 현재 노드 ($v$) 정보와 이웃 노드 (\(u\)) 정보를 GRU에 넣어서 현재 시점 노드를 업데이트 하는 방식입니다. 앞선 GNN과 차이점은 back-propagation through time (BPTT)를 사용한다는 점입니다. BPTT는 커다란 graph에 적용할 때 문제가 될 수 있는데, 왜냐하면 모든 노드의 intermediate state를 메모리에 저장해야하기 때문입니다.

Stochastic Steady-state Embedding (SSE)는 더 큰 그래프에 적용가능한 scalable 학습 알고리즘을 제시합니다. SSE는 노드의 hidden state를 stochastic, asynchronous 방식으로 업데이트 합니다. 이 알고리즘은 반복적으로 노드 배치를 sampling하고, 해당 배치에 대해서 gradient를 계산합니다. 안정성을 보장하기 위해 SSE의 recurrent function은 이전 state와 현재 state의 weighted average로 정의됩니다.

\[\mathbf{h}_v^{(t)}=(1-\alpha) \mathbf{h}_v^{(t-1)}+\alpha \mathbf{W}_{\mathbf{1}} \sigma\left(\mathbf{W}_{\mathbf{2}}\left[\mathbf{x}_v, \sum_{u \in N(v)}\left[\mathbf{h}_u^{(t-1)}, \mathbf{x}_u\right]\right]\right)\]

이전 시점의 현재 노드 ($v$)의 hidden state와 이전 시점의 이웃 노드 ($u$)와 현재 노드 정보($\mathbf{x}_v$)를 weighted average하는 방식입니다. 개념적으로는 중요하지만, 이론적으로 SSE의 수렴성은 증명되지 않았습니다.

4. Convolutional Graph Neural Networks

ConvGNN은 RecGNN과 관련이 깊습니다. 하나의 contraction 함수를 여러 layer에 반복적으로 적용하는 대신에, ConvGNN에서는 각 layer마다 다른 파라미터를 사용합니다.

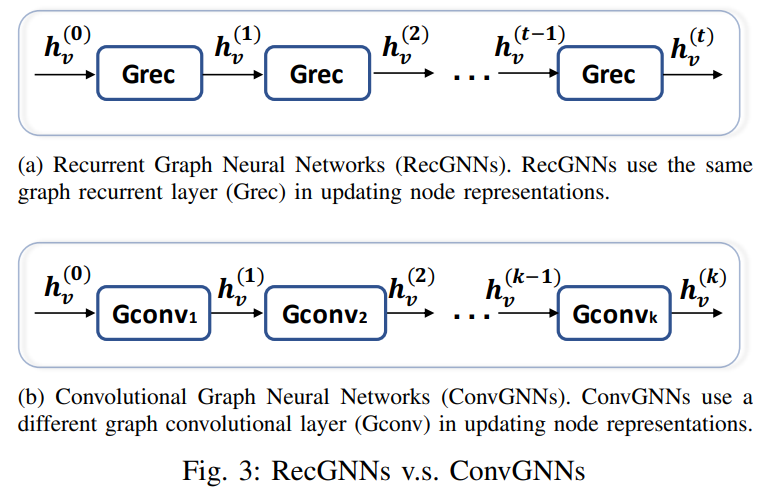
ConvGNN의 장점은 graph convolution 연산이 다른 뉴럴네트워크를 조합해서 사용하는 것보다 효율적이고 편리하기 때문입니다. 이로 인해 ConvGNN에 대한 관심이 최근에 증가했습니다.

ConvGNN은 spatial 기반과 spectral 기반으로 나누어집니다. Spectral 기반 방법은 filter를 사용해서 graph convolution을 정의하고, graph convolution을 graph에서 noise를 제거하는 수단으로 해석합니다. Spatial 기반 방법은 RecGNN 영향을 받아서 graph convolution이 information propagation 역할을 한다고 간주합니다. GCN이 spectral 기반과 spatial 기반의 차이를 연결해준 이후로, spatial 기반 방법이 효율성, 유연성, 일반성 때문에 빠르게 발전했습니다.

4.1. Spectral-based ConvGNNs

Spectral 기반 방법은 graph signal processing에 있는 견고한 수학적 기반에서 만들어졌습니다. 여기서는 그래프가 undirected라 가정하고, normalized graph Laplacian matrix를 \(\mathbf{L}=\mathbf{I}_{\mathbf{n}}-\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}\)으로 정의합니다. 여기서 \(\mathbf{D}\)는 \(\mathbf{D}_{i i}=\sum_j(\mathbf{A}_{i, j})\) 으로 정의된 대각행렬입니다. 그러면 \(\mathbf{L}\)은 real symmetric positive semi-definite 성질을 갖고 있기 때문에, \(\mathbf{L}=\mathbf{U} \boldsymbol{\Lambda} \mathbf{U}^T\) 형태로 eigen decomposition할 수 있습니다.

Graph signal processing에서, graph signal \(\mathbf{x}\in \mathbf{R}^n\)은 각 노드의 값들을 모아서 만든 feature vector입니다 (\(x_i\)는 \(i\)번째 node의 값). Signal \(\mathbf{x}\)에 대해서 graph Fourier 변환을 \(\mathscr{F}(\mathbf{x})=\mathbf{U}^T \mathbf{x}\)으로, inverse graph Fourier 변환을 \(\mathscr{F}^{-1}(\hat{\mathbf{x}})=\mathbf{U} \hat{\mathbf{x}}\)으로 정의하는데, 이는 graph signal을 normalized graph Laplacian 행렬의 eigenvector로 projection한 것 입니다. 이를 기반으로 입력 신호 \(\mathbf{x}\)와 filter \(\mathbf{g}\)에 대한 graph convolution을 다음과 같이 정의합니다.

\[\begin{aligned}\mathbf{x} *_G \mathbf{g} & =\mathscr{F}^{-1}(\mathscr{F}(\mathbf{x}) \odot \mathscr{F}(\mathbf{g})) \\& =\mathbf{U}\left(\mathbf{U}^T \mathbf{x} \odot \mathbf{U}^T \mathbf{g}\right)\end{aligned}\]

만약 \(\mathbf{g}_\theta=\operatorname{diag}\left(\mathbf{U}^T \mathbf{g}\right)\)라고 한다면 위의 식을 다음과 같이 바꿀 수 있습니다.

\[\mathbf{x} *_G \mathbf{g}_\theta=\mathbf{U g}_\theta \mathbf{U}^T \mathbf{x}\]

Spectral 기반 ConvGNN은 모두 위의 정의를 따르고, \(\mathbf{g}_{\theta}\)를 어떻게 선택하는지에 따라 차이가 있습니다.

Spectral Convolutional Neural Network (Spectral CNN)에서는 filter를 \(\mathbf{g}_\theta=\boldsymbol{\Theta}_{i, j}^{(k)}\) 으로 두고, graph convolutional layer를 다음과 같이 나타냅니다.

\[\mathbf{H}_{:, j}^{(k)}=\sigma\left(\sum_{i=1}^{f_{k-1}} \mathbf{U} \boldsymbol{\Theta}_{i, j}^{(k)} \mathbf{U}^T \mathbf{H}_{:, i}^{(k-1)}\right) \quad\left(j=1,2, \cdots, f_k\right)\]

여기서 k는 layer index 이고, $\mathbf{H}^{(k-1)} \in \mathbf{R}^{n \times f_{k-1}}$ 는 이전 시점의 그래프 신호이고, $f_{k-1}$은 입력 채널의 개수, $f_k$는 출력채널의 개수, $\Theta_{i, j}^{(k)}$는 학습가능한 파라미터로 이루어진 대각행렬입니다.

위의 식을 해석하면, 각 출력채널 ($j$) 마다 이전시점의 모든 입력 채널 ($i)$을 $j$번째 filter를 이용해서 graph convolution을 적용한다는 의미입니다. CNN에서 각 filter마다 이미지의 다른 특성을 추출하듯이, 여기서도 filter마다 그래프의 다른 특성을 추출하게 됩니다.

이 방법을 사용하려면 Laplacian matrix에 Eigen decomposition을 적용해야 하는데, 이로 인해서 3가지 제약사항이 있습니다. 첫째로 graph에 perturbation을 주면 eigen basis에 영향을 준다는 점이고, 두번째는 학습된 필터는 도메인에 따라 다르다는 점입니다. 이것의 의미는 어떤 구조에 학습된 필터는 다른 구조의 graph에 적용할 수 없다는 것입니다. 세번째는 eigen-decomposition은 $O\left(n^3\right)$만큼 계산량이 필요하다는 점입니다. 이후에 ChebNet과 GCN에서는 몇가지 근사방법을 통해 계산복잡도를 $O\left(n\right)$으로 줄입니다.

Chebyshev Spectral CNN (ChebNet)에서는 filter $\mathbf{g}_\theta$를 Chebyshev polynomial을 사용해서 근사합니다.

\[\mathbf{g}_\theta=\sum_{i=0}^K \theta_i T_i(\tilde{\boldsymbol{\Lambda}}), \text { where } \tilde{\boldsymbol{\Lambda}}=2 \boldsymbol{\Lambda} / \lambda_{\max }- \boldsymbol{I_n}\]

$\tilde{\Lambda}$의 값은 [-1, 1] 사이에 있고, Chebyshev polynomial은 다음과 같습니다.

\[T_i(\mathbf{x})=2 \mathbf{x} T_{i-1}(\mathbf{x})-T_{i-2}(\mathbf{x}), \;\text{where} \; T_0(\mathbf{x})=1, T_1(\mathbf{x})=\mathbf{x}\]

이를 이용해서 graph convolution을 표현하면 다음과 같습니다.

\[\mathbf{x} *_G \mathbf{g}_\theta=\mathbf{U}\left(\sum_{i=0}^K \theta_i T_i(\tilde{\mathbf{\Lambda}})\right) \mathbf{U}^T \mathbf{x}\] \[=\sum_{i=0}^K \theta_i T_i(\tilde{\mathbf{L}}) \mathbf{x}\] \[\text{where}\;\;T_i(\tilde{\mathbf{L}})=\mathbf{U} T_i(\tilde{\mathbf{\Lambda}}) \mathbf{U}^T, \;\;\,\,\tilde{\mathbf{L}}=2 \mathbf{L} / \lambda_{\max }-\mathbf{I}_{\mathbf{n}}\]

Spectral CNN과 비교해서 개선한 점은 ChebNet에서 정의된 filter는 locality 특성을 갖고있습니다. 즉 graph size와 상관없이 local feature를 추출할 수 있습니다. (보충)

Graph Convolutional Network (GCN)은 ChebNet의 first-order approximation입니다 $(K=1, \lambda_{max}=2)$. 그러면 ChebNet의 graph convolution을 다음과 같이 간소화할 수 있습니다.

\[\mathbf{x} *_G \mathbf{g}_\theta=\theta_0 \mathbf{x}-\theta_1 \mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}} \mathbf{x}\]

여기서 파라미터 개수를 줄이고 오버피팅을 예방하기 위해서 $\theta=\theta_0=-\theta_1$ 라는 가정을 해서 다음과 같이 위의식을 바꿉니다.

\[\mathbf{x} *_G \mathbf{g}_\theta=\theta\left(\mathbf{I}_{\mathbf{n}}+\mathbf{D}^{-\frac{1}{2}} \mathbf{A} \mathbf{D}^{-\frac{1}{2}}\right) \mathbf{x}\]

Multi-channel 입력과 출력을 허용하기 위해서, GCN은 compositional layer 형태로 표현이 가능합니다.

\[\mathbf{H}=\mathbf{X} *_G \mathbf{g}_{\boldsymbol{\Theta}}=f(\overline{\mathbf{A}} \mathbf{X} \boldsymbol{\Theta})\]

$\mathbf{I}_{\mathbf{n}}+\mathbf{D}^{-\frac{1}{2}} \mathbf{A D}^{-\frac{1}{2}}$값은 numerical instability를 초래한다는 실험적인 결과가 있어서, 이를 완화하기 위해 다음과 같은 normalization trick을 사용합니다.

\[\overline{\mathbf{A}}=\tilde{\mathbf{D}}^{-\frac{1}{2}} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-\frac{1}{2}} \text { with } \tilde{\mathbf{A}}=\mathbf{A}+\mathbf{I}_{\mathbf{n}} \text { and } \tilde{\mathbf{D}}_{i i}=\sum_j \tilde{\mathbf{A}}_{i j}\]

GCN은 또한 spatial-based 방법으로도 해석이 가능합니다. Spatial 관점에서 GCN은 이웃 노드의 feature information을 종합한 것으로 해석이 가능합니다.

\[\mathbf{h}_v=f\left(\boldsymbol{\Theta}^T\left(\sum_{u \in\{N(v) \cup v\}} \bar{A}_{v, u} \mathbf{x}_u\right)\right) \quad \forall v \in V\]

GCN을 점진적으로 개선한 방법들이 최근에 등장하고 있습니다. Adaptive Graph Convolutional Network (AGCN)에서는 관계를 adjacency matrix로 표현하지 않고 hidden structural relation을 학습합니다. 두 노드 feature를 입력으로 받아서 학습가능한 distance function을 통해 residual graph adjacency matrix라고 부르는 adjacency matrix를 만듭니다.

Dual Graph Convolutional Network (DGCN)에서는 두 개의 graph convolutional layer를 병렬적으로 합친 graph convolutional architecture를 제안했습니다. 두 레이어는 파라미터를 공유하고, normalized adjacency matrix $\overline{\mathbf{A}}$와 positive pointwise mutual information (PPMI) matrix를 사용합니다. PPMI는 graph에서 샘플링된 random walk를 통해 노드의 co-occurrence 정보를 추출합니다. PPMI 행렬은 다음과 같이 정의됩니다.

\[\mathbf{P P M I}_{v_1, v_2}=\max \left(\log \left(\frac{\operatorname{count}\left(v_1, v_2\right) \cdot|D|}{\operatorname{count}\left(v_1\right) \operatorname{count}\left(v_2\right)}\right), 0\right)\] \[\text { where } v_1, v_2 \in V,|D|=\sum_{v_1, v_2} \operatorname{count}\left(v_1, v_2\right)\]

$\operatorname{count}(\cdot)$함수는 random walk에서 node $v$와 node $u$가 동시로 등장하는 빈도를 반환합니다. (PPMI 해석 추가) Dual graph convolutional layer에서 얻은 output을 앙상블해서 DGCN은 여러 graph convolutional layer를 사용하지않고, local하고 global한 구조적인 정보를 인코딩합니다.

4.2. Spatial-based ConvGNNs

이미지에서 사용하는 전통적인 convolution 연산처럼, spatial 기반 방법은 노드의 spatial 관계를 기반으로 graph convolution을 정의합니다. 이 아이디어는 RecGNN에서 사용한 message passing과 유사하다.

Neural Network for Graphs (NN4G) 는 ConvGNN을 spatial 기반으로 설계한 첫번째 모델입니다. NN4G는 각 layer의 독립적인 파라미터를 두어서 graph dependency를 학습합니다. 여러 layer를 쌓으면서 노드의 이웃 범위가 점점 넓어지고, graph convolution을 통해 모든 이웃을 합친 정보를 생성합니다. 또한 residual connection을 사용해서 각 layer의 정보를 보존합니다.

Diffusion Convolutional Neural Network (DCNN) 은 graph convolution을 diffusion process로 간주합니다. 정보가 한 노드에서 다른 노드로 퍼질 때 특정한 확률을 갖고 몇번 전파된 이후에 information distribution이 평형상태에 도달한다고 가정합니다. DCNN은 diffusion graph convolution을 다음과 같이 정의합니다.

\[\mathbf{H}^{(k)}=f\left(\mathbf{W}^{(k)} \odot \mathbf{P}^k \mathbf{X}\right)\]

여기서 $f$는 activation function이고, $\mathbf{P}$는 probability transition matrix이고, $\mathbf{P}=\mathbf{D}^{-1} \mathbf{A}$ 형태로 계산이 가능합니다. DCNN은 $\mathbf{H}^{(1)}, \mathbf{H}^{(2)}, \cdots, \mathbf{H}^{(K)}$를 모두 concatenate한 값을 final model output으로 설정합니다. Diffusion process의 stationary distribution은 $\mathbf{P}$의 power series의 합이기 때문에, Diffusion Graph Convolution (DGC)는 다음과 같이 각 diffusion step마다 output을 합친 것입니다.

\[\mathbf{H}=\sum_{k=0}^K f\left(\mathbf{P}^k \mathbf{X} \mathbf{W}^{(k)}\right)\]

여기서 $K$는 diffusion step인데 높아질수록 넓은 범위까지 반영한다는 것입니다. $k$값이 커질수록 transition matrix가 여러번 곱해져서 확률값이 작아지기 때문에, 멀리있는 이웃노드들은 반영되는 비율이 적어집니다.

Partition Graph Convolution (PGC)는 현재 노드 이웃을 특정 기준에따라 Q개의 group으로 나누어서 Q개의 adjacency matrix를 생성합니다. 그래서 각 이웃노드 그룹마다 다른 파라미터를 사용해서 GCN을 다음과같이 적용합니다.

\[\mathbf{H}^{(k)}=\sum_{j=1}^Q \overline{\mathbf{A}}^{(j)} \mathbf{H}^{(k-1)} \mathbf{W}^{(j, k)}\] \[\;\;\;\;\,\,\,\,\,\,\,\text { where } \mathbf{H}^{(0)}=\mathbf{X}, \overline{\mathbf{A}}^{(j)}=\left(\tilde{\mathbf{D}}^{(j)}\right)^{-\frac{1}{2}}$ \tilde{\mathbf{A}}^{(j)}\left(\tilde{\mathbf{D}}^{(j)}\right)^{-\frac{1}{2}}\] \[\tilde{\mathbf{A}}^{(j)}=\mathbf{A}^{(j)}+\mathbf{I}\]

Q개의 group마다 Graph convolution을 적용하고 summation을 통해 최종적으로 현재 노드의 hidden state를 업데이트 합니다.

Message Passing Neural Network (MPNN)은 spatial 기반 ConvGNN의 일반적인 framework입니다. Graph Convolution을 message passing으로 간주해서, 정보가 한 노드에서 다른 노드로 직접 전달됩니다. Message passing 함수는 다음과 같이 정의됩니다.

\[\mathbf{h}_v^{(k)}=U_k\left(\mathbf{h}_v^{(k-1)}, \sum_{u \in N(v)} M_k\left(\mathbf{h}_v^{(k-1)}, \mathbf{h}_u^{(k-1)}, \mathbf{x}_{v u}^e\right)\right)\] \[\text { where } \mathbf{h}_v^{(0)}=\mathbf{x}_v\]

\(U_k(\cdot)\)와 \(M_k(\cdot)\)는 학습가능한 파라미터로 이루어진 함수입니다. 이전시점의 현재노드 hidden state \(\mathbf{h}_v^{(k-1)}\) 이랑 이웃노드 \(\mathbf{h}_u^{(k-1)}\), 엣지정보 \(\mathbf{x}_{v u}^e\)를 입력으로 받아서 변환하고 합친정보를 다시 $\mathbf{h}_v^{(k-1)}$와 합쳐서 $U_k$를 통해 변환하는 방식으로 업데이트를 합니다.

Graph Isomorphism Network (GIN)에서는 MPNN의 한계점을 발견했는데, MPNN 기반 방법에서그래프 임베딩을 통해 graph 구조를 구분하는게 불가능 하다는 것입니다. 이런 단점을 보완하기 위해 GIN에서는 중심노드의 가중치에 학습파라미터를 추가해서 graph convolution을 다음과 같이 수행합니다.

\[\mathbf{h}_v^{(k)}=M L P\left(\left(1+\epsilon^{(k)}\right) \mathbf{h}_v^{(k-1)}+\sum_{u \in N(v)} \mathbf{h}_u^{(k-1)}\right)\]

가중치 파라미터를 통해 중심노드와 주변노드를 구분해서 현재 노드를 업데이트를 합니다.

노드 이웃의 개수는 1개일 수도 있고 천개가 넘어갈 수도 있기 때문에, 모든 노드의 정보를 반영하는 것은 비효율 적일 가능성이 있습니다. 그래서 GraphSage에서는 각 노드에 반영될 이웃 노드의 개수를 고정시키고 sampling을 통해 convolution을 수행합니다.

\[\mathbf{h}_v^{(k)}=\sigma\left(\mathbf{W}^{(k)} \cdot f_k\left(\mathbf{h}_v^{(k-1)},\left\{\mathbf{h}_u^{(k-1)}, \forall u \in S_{\mathcal{N}(v)}\right\}\right)\right)\]

$S_{\mathcal{N}(v)}$는 노드 $v$의 이웃 노드의 랜덤 샘플입니다. 몇 개의 이웃노드를 랜덤으로 선택해서 이웃노드의 hidden state와 이전시점의 현재노드 hidden state $\mathbf{h}_v^{(k-1)}$를 합쳐서 convolution 연산을 수행합니다. Aggregation 함수 $f$는 mean, sum, max 함수처럼 노드 순서에 invariant한 성질을 가진 함수를 사용해야합니다.

Graph Attention Network (GAT)는 주변 노드들이 중심노드에 업데이트하는 비율이 동일하지 않고,미리 정해져 있지도 않습니다.

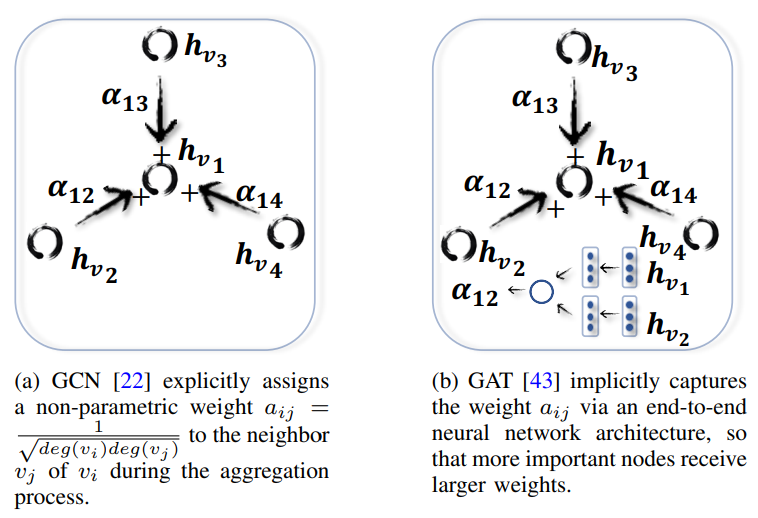
GCN은 업데이트 비율이 미리 정해져있고 GraphSage에서는 주변노드 반영비율이 모두 동일한데, GAT에서는 attention mechanism을 통해 각 노드의 반영비율이 유동적으로 모두 다르게 설정합니다.

\[\mathbf{h}_v^{(k)}=\sigma\left(\sum_{u \in \mathcal{N}(v) \cup v} \alpha_{v u}^{(k)} \mathbf{W}^{(k)} \mathbf{h}_u^{(k-1)}\right)\]

$\alpha_{v u}^{(k)}$값은 node $v$와 $u$의 연결 강도를 측정합니다. 추가적으로 GAT는 multi-head attention을 통해 모델의 표현력을 높였는데, GraphSage보다 node classification task에서 성능이 많이 좋아졌습니다.

GAT에서는 각 attention head마다 같은 분포를 갖는다고 가정하는데, Gated Attention Network (GANN)에서는 각 attention head마다 attention score를 따로 계산합니다. 다른 종류의 graph attention 모델도 있지만, 그들은 ConvGNN framework에 속하지 않아서 여기서 소개하지는 않습니다.

4.3. Improvement in terms of training efficiency

GCN같은 ConvGNN을 학습하려면 전체 graph data와 모든 노드의 중간 hidden state를 저장해야돼서 메모리가 많이 필요합니다. 메모리를 절약하기 위해 GraphSage는 batch-training algorithm을 제안했는데,

Fast Learning with Graph Convolutional Network (FastGCN)에서는 각 layer마다 고정된 수의 노드를 샘플링합니다. 그래서 각 layer마다 연결이 sparse하게 돼서 학습속도가 빨라집니다. Huang은 adaptive layer-wise sampling 기법을 제시하는데, top layer에 노드가 샘플링 되었을 때, 이를 기반으로 bottom layer 노드를 샘플링합니다. 더 복잡한 샘플링 기법을 사용해서 FastGCN보다 정확도를 높였습니다.

[Stochastic Training of Graph Convolutional Networks] (StoGCN)](https://arxiv.org/pdf/1710.10568.pdf)은 graph convolution의 receptive field 크기를 줄였습니다. Historic node representation을 통제변수로 사용했습니다. 노드 당 두개의 이웃노드만 사용해도 상당한 성능을 달성했습니다. 하지만 여전히 모든 노드의 intermediate state를 저장해야하기 떄문에 메모리 소비가 GCN과 같습니다.

Cluster-GCN 에서는 그래프 클러스터링 알고리즘을 사용해서 sub graph를 추출하고, sub-graph에 graph convolution을 적용합니다. 이웃노드 탐색 또한 sub-graph로 제한이 되어서 더 짧은 시간에 더 적은 메모리로 graph convolution 연산이 가능합니다.

s: 배치사이즈 / K: layer 수 /r: 각 노드마다 샘플된 이웃 노드의 수 / d: feature dimension

위의 표를 보면 GraphSage는 시간이 더 소모되지만 메모리가 절약됩니다. StoGCN의 시간복잡도는 가장 크고, 메모리 소비량도 GCN과 비슷합니다. 하지만 StoGCN은 r값이 작아도 좋은 성능을 유지할 수 있습니다. Cluster-GCN은 time complexity는 동일한데 메모리 소비량은 적습니다.

4.4. Comparison between spectral and spatial models

Spectral 모델은 graph signal processing의 이론적인 기반위에 세워졌습니다. 새로운 graph signal filter를 사용해서 새로운 ConvGNN을 만들 수 있지만, 일반적으로 spatial model이 효율성과 유연성 때문에 더 선호가 됩니다.

Spectral 기반 방법은 eigenvector를 계산해야하거나 전체 그래프를 한번에 다루어야 하는 경우가 많습니다. Spatial 모델은 information propagation을 통해 convolution을 수행하기 때문에, large graph에서도 적용이 가능합니다. 계산도 전체 그래프에 수행하는 대신에 일부 노드 배치에 대해서만 수행합니다.

또한 spectral 모델은 graph Fourier basis에 기반하기 때문에 새로운 그래프로 일반화가 되기 어렵습니다. Spectral 모델은 고정된 그래프를 가정하는데, 왜냐하면 Graph에 perturbation을 주면 eigen basis가 변하기 때문입니다. 반면 Spatial 기반 모델은 각 노드에 지역적으로 graph convolution 연산을 수행하기 때문에, weight이 다른 지역이나 구조로 공유될 수 있습니다.

마지막으로 spectral 기반 방법은 undirected graph로 한정이 되는데, spatial 기반 방법은 더 유연해서 다양한 graph(edge, directed graph, signed graph, hetereogeneous graph)를 입력으로 받을 수 있습니다.

	Spectral	Spatial
Scalability	Less (Due to eigenvector computation)	High
Generalization	Poor (Fixed graph assumption)	High
Available graph	Undirected	Undirected , Directed, edge, signed, heterogeneous

5. Graph Pooling Modules

GNN이 node feature를 생성하면 task에 따라 다르게 사용이 가능합니다. 모든 feature를 직접적으로 사용하는 건 계산량이 많아서 down-sampling을 사용합니다. 목적에 따라 다른 이름으로 사용이 되는데, 파라미터 크기를 줄이기 위해 down sampling하는 것은 pooling operation이라고 부르고, graph-level representation을 추출할 때 사용하면 readout operation이라고 부릅니다. 두 개의 mechanism은 유사합니다. 이번 챕터에서는 pooling을 down-sampling의 의미로 사용하겠습니다.

일반적으로 mean/max/sum pooling이 가장 기초적이고 효과적인 down sampling 방법입니다. DCGNN에서는 SortPooling이라는 pooling 방법을 제시했는데, 이 방법은 노드의 순서를 그래프 구조에서 노드의 역할에 따라 의미적으로 배열해서 풀링을 수행합니다.

Differentiable pooling (DiffPool)에서는 그래프의 계층적인 표현을 생성합니다. 이전의 corasening 기반 방법과는 다르게 DiffPool은 각 layer $k$ 마다 cluster assignment matrix $S$를 다음과 같이 학습가능하게 만듭니다.

\[\mathbf{S}^{(k)}=\operatorname{softmax}\left(\operatorname{Conv} G N N_k\left(\mathbf{A}^{(k)}, \mathbf{H}^{(k)}\right)\right)\]

이런 방법의 중심이 되는 생각은 그래프의 위상적인 정보와 feature 정보를 동시에 고려해서 node assignment를 수행한다는 점입니다. 하지만 DiffPool의 단점은 풀링 이후에 dense graph를 생성해서 계산복잡도가 $O\left(n^2\right)$이 됩니다.

SAGPool에서는 node feature와 graph topology를 모두 고려하면서 self-attention 방식응로 풀링을 수행합니다.

풀링 연산은 그래프 크기를 줄일 수 있는 효율적인 연산입니다. 풀링을 통해 계산복잡도를 어떻게 낮출 수 있는지는 여전히 열러있는 문제입니다.

6. Discussion of Theoretical Aspects

여기서는 GNN의 이론적인 기반에 대해 살펴보겠습니다.

6.1. Shape of receptive field

노드의 receptive field는 마지막 노드 representation에 기여한 노드의 집합입니다. 여러 spatial graph convolutional layer를 사용하면 노드의 receptive field는 커집니다. Micheli는 고정된 크기의 spatial graph convolutional layer를 사용해서 모든 노드를 커버하는 receptive field를 만들 수 있다고 증명했습니다. 그 결과, ConvGNN은 몇개의 local graph convolutional layer를 사용해서 global information을 추출할 수 있습니다.

6.2. VC dimension

VC dimension은 모델에의해 분해될 수 있는 최대 점의 수로 정의되는, 모델 복잡도를 측정하는 방법입니다. GNN의 VC dimension을 분석하는 몇가지 논문이 있었습니다. 모델 파라미터 개수 p와 노드 수 n이 주어졌을 때, Scarselli는 GNN에서 tangent hyperbolic 혹은 sigmoid activation을 사용했을 경우에 VC dimension이 $O\left(p^4 n^2\right)$라고 주장합니다. 이 결과는 GNN의 모델 복잡도가 p와 n에 따라 빠르게 증가한다는 것을 암시합니다.

6.3. Graph isomorphism

두 그래프는 위상적으로 동일하면 isomorphic합니다. non-isomorphic graph $G_1, G_2$가 있을 때, Xu는 GNN이 $G_1$과 $G_2$를 다르게 임베딩한다면 Weisfeiler-Lehman (WL) test를 통해 두 그래프가 non-isomorphic하다고 밝혀낼 수 있다고 합니다. GCN이나 GraphSage같은 일반적인 GNN에서는 두 그래프 구조를 구분하는게 불가능하다고 말합니다. 만약 aggregation function과 readout function이 injective 하다면, GNN을 통해 두 그래프를 구분할 수 있다고 합니다.

6.4. Equivariance and invariance

GNN은 node-level task를 수행할 떄는 equivariant해야하고, graph-level task를 수행할 때는 invariant해야 합니다.

$Q$가 임의의 permutation matrix라 하고, $f(\mathbf{A}, \mathbf{X})$가 GNN이라고 하면$f\left(\mathbf{Q A Q}{ }^T, \mathbf{Q X}\right)=\mathbf{Q} f(\mathbf{A}, \mathbf{X})$을 만족할 때 f는 equivariant하고, $f\left(\mathbf{Q A Q}^T, \mathbf{Q X}\right)=f(\mathbf{A}, \mathbf{X})$를 만족할 떄 f는 invariant 합니다. Equivariance와 invariance 성질을 갖기 위해 GNN component는 노드 순서에 영향을 받지 않아야 합니다.

7. Graph Autoencoders (GAE)

Graph Autoencoder는 노드를 feature space로 임베딩하고 feature space에서 graph 정보를 생성합니다. GAE는 네트워크 임베딩 혹은 새로운 그래프를 생성할 때 사용할 수 있습니다.

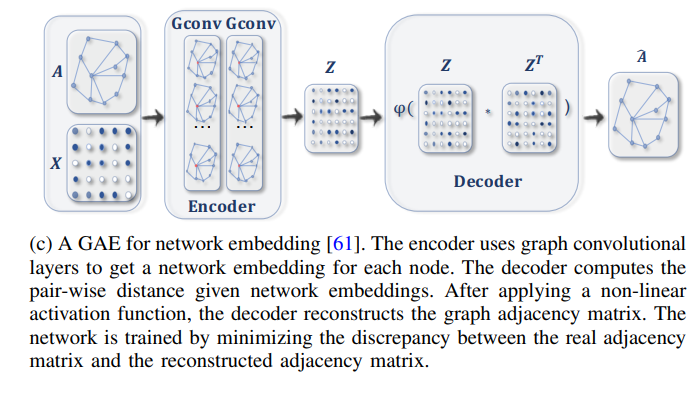
7.1. Network Embedding

네트워크 임베딩은 low-dimension에서 노드의 위상적인(topological) 정보를 보존한 채로 노드를 저차원 벡터로 표현한 것입니다. GAE는 인코더를 통해 네트워크 임베딩을 학습하고 디코더를 통해 PPMI와 인접행렬처럼 그래프의 위상적인 정보를 네트워크 임베딩에 반영합니다.

초기 접근은 주로 multi-layer perceptron을 이용했습니다. SDNE에서는 인코더를 통해 노드의 first-order proximity(현재 노드와 직접적으로 연결된 노드 정보)와 second-order proximity(이웃 노드들의 이웃 노드 정보)를 반영했습니다.

Second-order proximity를 좀 더 자세하게 설명하자면, 만약 어떤 노드 pair $(u, v)$가 있을 때 두 노드를 연결하는 edge의 weight $w_{u,v}$는 first-order proximity입니다. 그러면 모든 이웃 노드를 반영해서 하나의 벡터 $p_u = (w_{u,1}, …, w_{u,|V|})$를 만들 수 있습니다. Second-order proximity는 $p_u$와 $p_v$ 사이에 유사도를 의미합니다. 이것의 의미를 해석하면, 공유하고 있는 이웃노드들이 많으면 두 노드는 유사하다고 판단하는 것입니다.

네트워크 임베딩에 First-order proximity를 반영하기 위해서 인접한 두 노드의 임베딩이 같도록 다음과 같은 loss function을 사용했습니다.

\[L_{1 s t}=\sum_{(v, u) \in E} A_{v, u}\left\|e n c\left(\mathbf{x}_v\right)-e n c\left(\mathbf{x}_u\right)\right\|^2\]

위의 loss function은 이웃하는 노드들의 임베딩을 유사하게 만들어주는 역할을 하고, 네트워크의 local structure 정보를 임베딩에 반영하게 됩니다.

그리고 second-order proximity를 반영하기 위해서 입력 노드와 생성된 노드가 같아지도록 다음과 같은 loss function을 사용했습니다.

\[L_{2 n d}=\sum_{v \in V}\left\|\left(\operatorname{dec}\left(\operatorname{enc}\left(\mathbf{x}_v\right)\right)-\mathbf{x}_v\right) \odot \mathbf{b}_v\right\|^2\] \[\text { where } b_{v, u}=1 \text { if } A_{v, u}=0, b_{v, u}=\beta>1 \text { if } A_{v, u}=1\]

여기서 두 노드가 연결이 되어있으면 1보다 큰 가중치를 주고, 연결되어있지 않으면 1만큼 반영하는 식으로 가중치를 할당했습니다. Second-order proximity를 통해서는 네트워크의 global structure 정보를 임베딩에 반영하게 됩니다.

SDNE는 노드 사이의 연결성에 관련된 정보만 고려를 했습니다. 노드 자체가 갖고있는 feature정보를 사용하지 않았는데, GAE*에서는 노드의 구조적인 정보와 노드 feature 정보를 모두 반영해서 인코딩하려고 GCN을 encoder로 사용하는 방법을 제시했습니다.

\[\mathbf{Z}=e n c(\mathbf{X}, \mathbf{A})=G \operatorname{conv}\left(f\left(G \operatorname{conv}\left(\mathbf{A}, \mathbf{X} ; \boldsymbol{\Theta}{\mathbf{1}}\right)\right) ; \boldsymbol{\Theta}{\mathbf{2}}\right)\]

ㅇ여기서 \(\mathbf{Z}\)는 네트워크 임베딩 행렬이고 \(f\)는 ReLU, \(Gconv\)는 graph convolutional layer 입니다. 이렇게 네트워크를 임베딩하고, decoder에서는 네트워크 임베딩에서 인접행렬 \(A\)를 복원하는 것을 목표로 합니다.

\[\hat{\mathbf{A}}_{v, u}=\operatorname{dec}\left(\mathbf{z}_v, \mathbf{z}_u\right)=\sigma\left(\mathbf{z}_v^T \mathbf{z}_u\right)\]

그래서 GAE*에서는 실제 인접행렬 \(A\)와 모델을 통해 다시 만들어진 행렬 \(\hat{A}\)사이에 cross entropy를 낮추는 방향으로 학습이 진행이 됩니다.

그런데 논문에서는 단순히 인접행렬을 복원하는 방향으로 학습을 하면 overfitting이 생길 수 있다고 생각해서, 해당 문제를 해결할 수 있는 Variational Graph Autoencoder (VGAE)를 제안합니다. VGAE에서는 다음과 같은 lower bound를 최대화 하는 방향으로 학습을 진행합니다.

\[\begin{aligned}& L=E_{q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A})}[\log p(\mathbf{A} \mid \mathbf{Z})]-K L[q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A}) \| p(\mathbf{Z})] \\\\& \;\;\;\;\;\;\;\; p\left(A_{i j}=1 \mid \mathbf{z}_i, \mathbf{z}_j\right)=\operatorname{dec}\left(\mathbf{z}_i, \mathbf{z}_j\right)=\sigma\left(\mathbf{z}_i^T \mathbf{z}_j\right) \\& \;\;\;\;\;\;\;\; q(\mathbf{Z} \mid \mathbf{X}, \mathbf{A})=\prod_{i=1}^n q\left(\mathbf{z}_i \mid \mathbf{X}, \mathbf{A}\right) \text { with } q\left(\mathbf{z}_i \mid \mathbf{X}, \mathbf{A}\right)=N\left(\mathbf{z}_i \mid \mu_i, \operatorname{diag}\left(\sigma_i^2\right)\right)\end{aligned}\]

여기서 \(p(\mathbf{Z})\)는 factorized gaussian prior입니다. VGAE에서는 VAE처럼 인코더의 아웃풋을 정규분포 파라미터를 통해 추정합니다. 실제로 link prediction 실험 결과에서도 3개 dataset 중 2개 dataset (Cora, Citeseer)에서 VGAE가 GAE보다 성능이 좋았고, 노드 feature 정보를 사용하지 않았을 때 보다 사용했을때는 모든 데이터셋에 대해서 성능이 향상되었습니다.

GAE*와 유사하게 GraphSage에서는 2개의 GCL을 통해 노드 피처를 인코딩합니다. GAE*와 차이점은 recon-struction error를 사용하지 않고, 두 노드의 관계정보를 negative sampling을 통해 임베딩에 반영합니다.

\[L\left(\mathbf{z}_v\right)=-\log \left(\operatorname{dec}\left(\mathbf{z}_v, \mathbf{z}_u\right)\right)-Q E{v_n \sim P_n(v)} \log \left(-\operatorname{dec}\left(\mathbf{z}_v, \mathbf{z}_{v_n}\right)\right)\]

\(P_n(v)\)는 negative sample distribution이고, Q는 negative sample 개수입니다. 위의 loss function은 이웃 노드들에 대해서는 유사한 embedding이 생성되는 방향으로, negative sample(이웃하지 않은 노드)들에 대해서는 유사하지 않는 embedding이 생성되는 방향으로 학습이 진행됩니다.

지금까지 소개한 방법들은 link prediction 문제를 해결하면서 네트워크 임베딩을 학습했스비다. 하지만 sparse graph의 경우에는 positive node pair의 수가 negative node pair보다 현저하게 작아서 이웃 노드 임베딩이 유사해지지 않을 가능성이 생깁니다. 이 문제를 해결하기 위해서 그래프를 random permutation 혹은 random walk를 사용해서 sequence 형태로 변형하는 방향으로 진행되는 연구도 있습니다.

Deep Recursive Network Embedding (DRNE)에서는 regular invariance라는 개념을 사용해서 네트워크 임베딩을 수행합니다. Regular invariance란 어떤 두 노드가 공통된 이웃 노드가 존재하지 않더라도, 비슷한 역할을 수행하는 노드입니다. 다시말해서, 네트워크 구조와 상관없이 그 자체로 노드가 유사하면 두 노드는 regular invariant하다고 정의합니다.

Regular invariant 노드를 유사하게 임베딩하기 위해서 DRNE는 노드의 네트워크 임베딩이 이웃한 네트워크 임베딩의 aggregation을 근사한 것이다라고 가정을 합니다. 그리고 이웃노드를 degree별로 오름차순으로 정렬해서 LSTM을 사용해서 노드의 이웃을 다음과 같이 aggregate 합니다.

\[L=\sum_{v \in V}\left\|\mathbf{z}_v-\operatorname{LSTM}\left(\left\{\mathbf{z}_u \mid u \in N(v)\right\}\right)\right\|^2\]

위의 식은 LSTM에서 임베딩을 생성하는 것이 아니라, 노드의 임베딩을 이웃노드의 임베딩을 aggregation해서 생성하고 있습니다. 조금 이해가 안가는 점은degree를 기준으로 노드 임베딩을 정렬해서 LSTM을 통해 aggregation 하는 것이 regular invariance정보와 어떤 관련이 있는지 잘 이해가 가지 않았습니다.

7.2. Graph Generation

GAE는 학습 과정을 통해 graph에 대한 generative distribution을 학습할 수 있습니다. Graph generation을 위한 GAE는 대부분 molecular graph generation 문제를 해결하기 위해 제안되었습니다. Graph generation 접근방법에는 sequential 방식과 global 방식 두가지가 있습니다.

Sequential 방식에는 Deep Generative Model of Graphs (DeepGMG)라는 방법이 있는데, 이 방법은 그래프의 확률을 모든 가능한 node permutation의 합으로 가정합니다.

\[p(G)=\sum_\pi p(G, \pi)\]

여기서 \(\pi\)는 노드 순서를 의미합니다. 이 확률은 그래프에서 모든 노드와 엣지의 join probability를 반영합니다. DeepGMG에서 그래프를 생성할 때 순차적으로 결정을 내리는데, 주로 노드 혹은 엣지를 추가할지 말지, 어떤 노드를 추가할지를 결정합니다. 노드 state 혹은 graph state에 따라 node나 edge를 생성하는 결정과정이 달라집니다.

Global 방식에서는 그래프를 한번에 출력합니다. Graph Variational Autoencoder (GraphVAE)에서는 독립적인 확률변수로 노드와 엣지의 존재여부를 모델링 하고, 다음과 같은 lower bound를 최대화 합니다.

\[L(\phi, \theta ; G)=E_{q_\phi(z \mid G)}\left[-\log p_\theta(G \mid \mathbf{z})\right]+K L\left[q_\phi(\mathbf{z} \mid G) \| p(\mathbf{z})\right]\]

ConvGNN을 인코더로 삼고, multi-layer perceptron을 decoder로 사용해서 인접 행렬과 함께 그래프를 생성합니다. 이런 방식은 생성된 그래프의 global property (graph connectivity, validity) 같은 요소를 통제하기가 어렵습니다.

8. Spatial-Temporal Graph Neural Networks (STGNN)

현실세계에서 그래프 구조나 그래프에 들어오는 input은 대부분 dynamic한 성질을 갖고있습니다. STGNN은 그래프의 dynamicity를 반영하는 방법입니다. STGNN은 그래프의 spatial, temporal dependency를 동시에 학습합니다. 주로 future node value를 예측하거나, 현재 그래프의 label을 예측하는 데 사용이 됩니다. 이 방법은 RNN 기반 방법과 CNN 기반 방법 두가지가 있습니다.

대부분 RNN 기반 방법은 Graph convolution을 통해 현재 시점 입력과 이전 시점 hidden state를 다음 state로 넘기는 방식으로 다음과 같이 이루어져 있습니다.

\[\mathbf{H}^{(t)}=\sigma\left(G \operatorname{conv}\left(\mathbf{X}^{(t)}, \mathbf{A} ; \mathbf{W}\right)+G \operatorname{conv}\left(\mathbf{H}^{(t-1)}, \mathbf{A} ; \mathbf{U}\right)+\mathbf{b}\right)\]

위의 식은 현재 시점 입력 $\mathbf{X}^{(t)}$와 이전 시점 hidden state $\mathbf{H}^{(t-1)}$이 graph convolution을 통해서 현재 시점의 hidden state로 변하는 과정입니다.

RNN 기반인데 다른 방식의 연구는 node-level RNN과 edge-level RNN을 동시에 사용하는 방법입니다. Structural-RNN에서는 각 time step마다 node-RNN을 사용해서 노드의 temporal 정보를 반영하고, edge-RNN을 사용해서 edge의 temporal 정보를 반영합니다. 그리고 spatial 정보를 통합하기 위해서 edge-RNN의 출력값을 node-RNN의 입력으로 집어넣습니다. 이를 통해 각 time step마다 node label을 예측하는 모델을 제안했습니다.

RNN 기반 방법들은 순차적으로 데이터가 모델에 전달이 되기 때문에 시간이 많이 소모되고, gradient explosion/vanishing 문제도 존재합니다. 그래서 CNN 기반 방법에서는 순차적으로 데이터를 처리하지 않고 병렬적으로 처리해서 spatial temporal graph를 학습합니다.

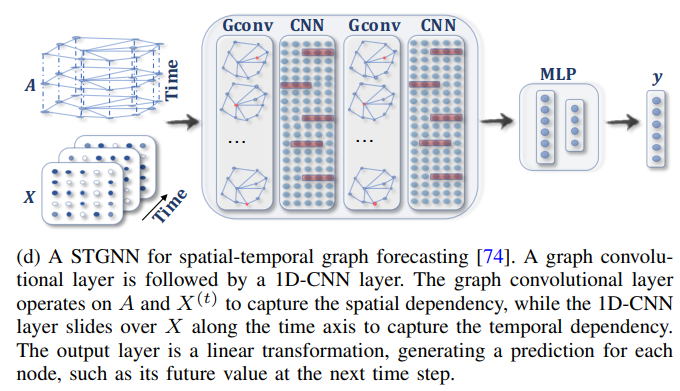
위의 그림처럼 CNN 기반 방법은 Graph Convoluion을 통해 spatial 정보를 학습하고 1D-CNN을 통해 temporal 정보를 학습합니다. 1D-CNN은 각 노드마다 시간축을 따라 convolution을 진행해서 temporal 정보를 aggregation 합니다.

지금까지 소개한 방법들은 그래프 구조가 미리 정해진 상태였습니다. 하지만 spatial-temporal setting에서는 그래프 데이터를 통해서 graph structure를 학습할 수 있습니다. Graph WaveNet에서는 graph convolution을 수행할 때 다음과 같이 정의된 self-adaptive adjacency matrix를 사용했습니다.

\[\mathbf{A}_{a d p}=\operatorname{SoftMax}\left(\operatorname{ReLU}\left(\mathbf{E}_1 \mathbf{E}_2^T\right)\right)\]

\(\mathbf{E_1}\) 은 source node embedding을 가리키고, \(\mathbf{E}_2\)는 target node embedding을 가리킵니다. \(\mathbf{E}_1\) 과 \(\mathbf{E}_2\) 를 곱해서 source node와 target node 사이에 dependency weight을 얻을 수 있고, 이를 통해 인접 행렬을 추정하는 방식입니다. Graph WaveNet은 인접행렬이 주어지지 않아도 좋은 성능을 내는 결과를 보여주었습니다.

GaAN에서는 attention mechanism을 통해 dynamic spatial dependency를 학습했습니다. Attention을 통해서 연결된 두 노드 사이에 edge weight를 업데이트를 했습니다. ASTGCN에서는 spatial 뿐만 아니라 temporal 정보 까지도 attention mechanism을 이용해서 학습을 했습니다. 이렇게 spatial dependency를 학습하는 방법들의 단점은 spatial dependency를 계산할 때 모든 노드들에 대해서 계산해야 하므로 $O(n^2)$정도의 비용이 필요하다는 점입니다.

9. Application

9.1. Computer vision

Computer vision에서는 scene graph generation, point cloud classification, action recognition 에서 사용이 됩니다.

Scene graph generation model은 물체사이에 의미적인 관계를 semantic graph로 나타내는 것을 목표로 합니다. 그리고 scene graph가 주어졌을 때 실제 이미지를 생성하는 방식도 존재합니다.

Point cloud를 분류하고 segmentation하는 작업을 통해 LiDAR 장치는 주위 환경을 인식할 수 있게 되었습니다. Point cloud를 k-nearest neighbor graph혹은 super point graph로 변환하거나, ConvGNN을 통해 point cloud의 topological structure를 조사할 수도 있습니다.

비디오에서는 사람의 관절을 graph 형태로 표현해서 사람의 행동을 time series graph로 표현할 수 있습니다. 각 관절이 node이고 뼈를 통해 연결이 된 것을 edge로 표현해서 graph를 생성합니다. 이렇게 time series graph 데이터를 통해서 사람의 행동을 인식할 수 있는 모델을 학습할 수 있습니다.

9.2. Natural Language Processing

NLP에서 GNN은 주로 text classification에 사용이 됩니다. 단어나 문서간의 상호관계를 GNN을 통해 파악하는 역할로 사용합니다. 언어 데이터가 순차적인 특성을 갖고있지만, 문장 하나에서도 단어마다 서로 관련이 있기 때문에 graph 구조로 표현이 가능합니다. 문법 구조를 표현하는 graph를 학습하거나 아니면 추상적인 단어들로 구성된 semantic graph에서 같은 의미를 가진 문장들을 생성할 때 GNN을 사용합니다.

9.3. Traffic

정확하게 도로의 교통량, 혼잡도, 차량의 속도를 예측하는 것은 교통시스템을 설계하는데 있어서 중요합니다. 몇몇 논문들은 traffic network를 spatial-temporal graph로 간주를 해서 traffic을 예측했는데, 도로위의 센서들을 노드, 센서 사이의 거리를 edge, 각 센서의 평균 traffic speed를 dynamic input feature로 삼아서 traffic speed를 STGNN을 이용해서 예측했습니다.

9.4. Recommender Systems

그래프 기반 추천 시스템은 아이템과 유저를 노드로 간주합니다. 그리고 아이템-아이템, 아이템-유저, 유저-유저 사이의 관계를 graph 형태로 표현해서 좀 더 성능이 좋은 추천을 가능하게 했습니다. 주로 GNN을 통해 아이템과 유저 사이에 link prediction을 통해 아이템을 추천합니다.

9.5. Chemistry

화학분야에서 연구자들은 GNN을 사용해서 분자나 혼합물의 그래프 구조를 예측합니다. 원자를 노드로 간주하고 화학적인 결합을 edge로 생각해서 molecular fingerprint를 학습하거나, protein interface를 예측하거나 새로운 화학적 혼합물을 합성하는데 사용합니다.

10. Future Directions

10.1. Model Depth

Li et al., 2018 에서 ConvGNN의 성능은 graph convolution layer 수가 많아질수록 감소한다고 밝혔습니다. Graph convolution은 인접 노드가 서로 유사해지도록 만드는데, graph convolution이 무한대만큼 존재하면 결국 모든 노드들이 하나의 representation으로 수렴하게 될 것이라고 주장하고 있습니다. 그래서 그래프 데이터를 학습할 때 깊이를 어느정도로 설정해야할지에 관해서 아직까지 의견이 분분합니다.

10.2. Scalability trade-off

GNN의 scalability는 이웃노드를 sampling 하거나 clustering 하는 것을 통해 확보합니다. 이웃노드를 sampling 하면 계산하는 비용은 감소하지만 중요한 정보를 포함하고 있는 이웃 노드의 정보를 반영하지 못하게 됩니다. 또한 clustering을 통해 중요한 구조적인 패턴 정보를 손실하게 됩니다. 그래서 정보를 많이 일지 않고 계산량을 줄이는 방법에 관해서도 연구가 필요합니다.

10.3. Heterogenity

대부분 GNN은 homogeneous graph를 가정합니다. 그래서 현재 GNN을 heterogenous graph에 적용하는 것은 어렵습니다. Heterogenous graph는 다른 타입의 노드나 엣지가 포함된 그래프입니다. 예를들어 이미지나 텍스트를 모두 입력으로 받는 그래프 같은 것입니다. 그래서 heterogenous graph에 GNN을 적용하려는 연구도 필요합니다.

10.4. Dynamicity

STGNN을 통해 graph의 dynamicity가 부분적으로 다루어졌지만, dynamic spatial relation의 경우에 graph convolution을 어떻게 적용해야할지에 관해서 고려하는 연구가 적어서, 이 방향의 연구도 필요합니다.