A survey of Quantization Methods for Efficient Neural Network 정리

1. Neural Network 최적화 연구방향들

1.1. 효율적인 네트워크 설계

Micro-architecture 관점에서는 kernel type을 depth-wise convolution 혹은 low-rank factorization을 사용하는 방법이 있고, Macro-architecture 관점에서는 residual, inception 같은 network를 사용하는 방법이 있다. 이런 방향들의 연구는 대부분 새로운 architecture를 발견하는 것이기 때문에, 작업이 수동적으로 이루어져서 확장가능(Scalable)하지 않다. 그래서 최근에는 Automated Machine Learning (AutoML)이나 Neural Architecture Search (NAS) 처럼 자동으로 효율적인 architecture를 찾는 방법들이 연구되고 있다.

1.2. 하드웨어를 고려한 네트워크 설계

Latency와 energy 관점에서 네트워크의 오버헤드는 하드웨어 영향을 많이 받는다. 이런 방향도 처음에는 수동적으로 했지만 점차 자동으로 변하고 있다.

1.3. Pruning

memory 사용량과 계산비용을 줄이는 방법 중 pruning이 있다. Pruning은 중요하지 않은 뉴런 (neurons with small saliency)을 제거해서 sparse computational graph를 생성한다. Pruning은 크게 두 가지 방법으로 나뉜다.

• Unstructured Pruning

Neuron 단위로 파라미터를 제거하는 방법. 이런 방법은 sparse matrix 연산으로 이어지게 되는데, 이 연산은 가속화하기 어렵고 연산속도가 메모리에 의해 결정된다고 (memory-bound) 알려져있다.

• Structured Pruning

그룹 단위로 파라미터를 제거하는 방법. 각 layer의 input과 output shape를 변화시킨다. 하지만 너무 많이 할 경우 performance가 떨어진다는 단점이 있다.

1.4. Knowledge Distillation

커다란 모델을 훈련하고 해당 모델을 teacher로 삼아서 작은 모델을 훈련하는 방법. Teacher에의해 생성어된 soft probability를 이용해서 훈련을 한다. Distillation 방법은 quantization이나 pruning에 비해 압축율 대비 성능이 낮다. 그래서 주로 quantization이나 pruning과 결합해서 사용이 된다.

1.5. Quantization

네트워크를 학습하거나 추론할 때 꾸준히 좋은 성공을 거두는 방법입니다. 이 논문에서는 대부분 inference에 관한 quantization 방법이지만, quantization 기법은 training 기법에서 성공을 더 많이 거두었다고 합니다. 특히 half-precision이나 mixed-precision training 기법이 네트워크를 가속하는 주요한 방법입니다. 하지만 half-precision보다 더 밑으로 학습하는 방법은 세세한 tuning 방법이 필요해서, 최근 연구 방향은 inference 측면에 초점을 두고 있습니다.

2. Quantization 기법 종류

문제정의

일반성을 잃지않고 Supervised Learning이라고 가정을 하자. 뉴럴 네트워크가 L개의 layer를 갖고있고, 각 layer의 파라미터를 $\theta = {W_1,W_2,…,W_L}$ 라고 했을 때 loss function을 다음과 같이 정의할 수 있다.

\[\mathcal{L}(\theta)=\frac{1}{N} \sum_{i=1}^N l\left(x_i, y_i ; \theta\right)\]

Quantization의 목표는 모델의 generalization power / accuracy에 영향을 주지 않은 채로 $\theta$와 intermediate activation($h$)의 precision을 낮추는 것이다. $\theta$와 $h$에 어떤 Quantization 함수를 적용하는지에 따라 방법이 나뉜다.

2.1. Uniform Quantization

\[Q(r) = Int(r/S)-Z \tag{1}\]

실수 r을 scale factor S로 나누고, zero point를 맞춰주기 위해 Z를 빼준다. 이러면 위의 그림처럼 실수가 scale factor 간격 (주황색 점을 잇는 선분)마다 속한 값으로 변경이된다.

2.2. Symmetric and Asymmetric Quantization

위의 (1)번 식에서 scaling factor S에 따라 실수가 대응되는 정수 partition 개수가 달라진다.

\[S=\frac{\beta-\alpha}{2^b-1} \tag{2}\]

여기서 $[\alpha,\beta]$는 clipping range를 나타내는데, 이 범위에 속한 실수값들에 대해서만 quantization을 적용하겠다는 의미이다. Clipping range를 결정하는 과정을 calibration이라고 한다.

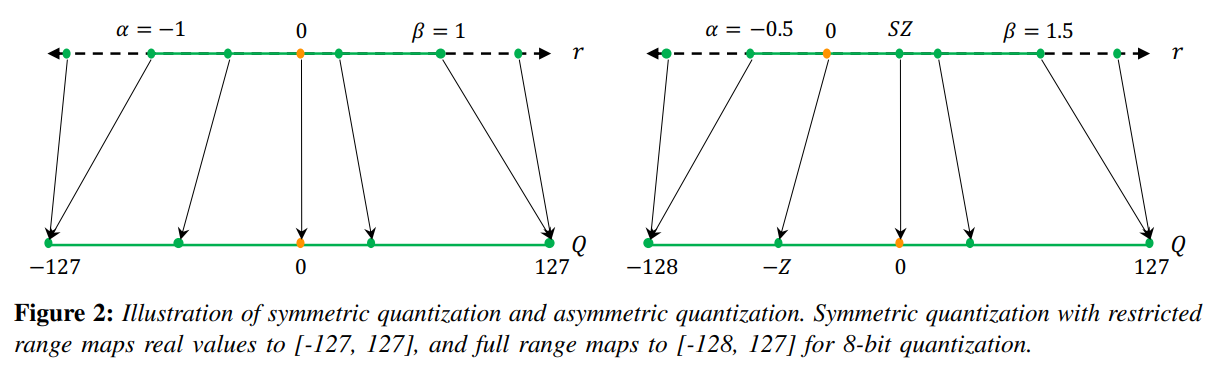
Symmetric quantization은 $\alpha = -\beta$로 두는 방법이다. 이러면 zero point를 조정할 필요가 없어서 Z값이 0이 되고, (1)번식에서 Z를 빼는 추가적인 계산 비용이 소모되지 않는다는 장점이 있다. 하지만 ReLU처럼 output이 한쪽으로 쏠려있는 실수값에 symmetric quantization을 적용하게 되면 asymmetric에 비해 resolution이 작아지게된다. 이런 단점에도 불구하고 뺄셈연산 하나를 줄이는게 inference할 때 계산비용을 줄여줘서 실제로 많이 활용된다.

Asymmetric quantization은 $\alpha = r_{min}, \beta = r_{max}$로 두는 방법이다. 그래서 symmetric quantization 보다 더 넓은 범위 실수값에 대해서 quantization을 적용할 수 있고, 값이 한쪽으로 치우쳐진 경우에 대해서 더 높은 resolution으로 데이터 표현이 가능하다. 하지만 zero point가 0이 아니기 때문에 quantization 과정에서 추가적으로 Z값을 빼줘야한다.

두 Quantization 기법은 모두 outlier에 취약하다. clipping range를 벗어난 입력이 inference할 때 들어올 경우 문제가 된다. 그래서 min/max value로 $\alpha, \beta$를 설정하지 않고, i번째로 가장 큰/작은 값으로 설정하거나 실수값과 quantized value 사이에 KL divergence가 최소가되는 $\alpha, \beta$를 선택하는 기법들이 있다.

2.3. Static and Dynamic Quantization

Symmetric, Asymmetric quantization 기법은 모든 layer에서 $\alpha, \beta$ 값이 동일하고 그 값들이 네트워크가 forward pass 되기 전에 미리 계산이 되는 static quantization 기법이다. 하지만 각 layer의 activation map마다 실수범위가 다르고 각 batch마다 값이 다르기 때문에, 값을 미리 하나로 고정시키는 것은 accuracy 측면에서 성능이 떨어진다.

그래서 inference 하는 과정에서 각 batch, layer마다 $\alpha, \beta$ 값을 결정해주는 방법을 dynamic quantization이라고 한다. 이 방법은 정확도 측면에서 성능이 좋아지지만 계산량이 추가적으로 소모돼서 자주 쓰이지 않는다.

2.4. Quantization Granularity

컴퓨터 비전에서 convolution 연산을 할 때 layer마다 filter 값의 범위가 다르다. 그래서 네트워크 파라미터를 어떤 단위(Granularity)로 clipping 하는지에 따라 quantization 기법이 나뉘어진다.

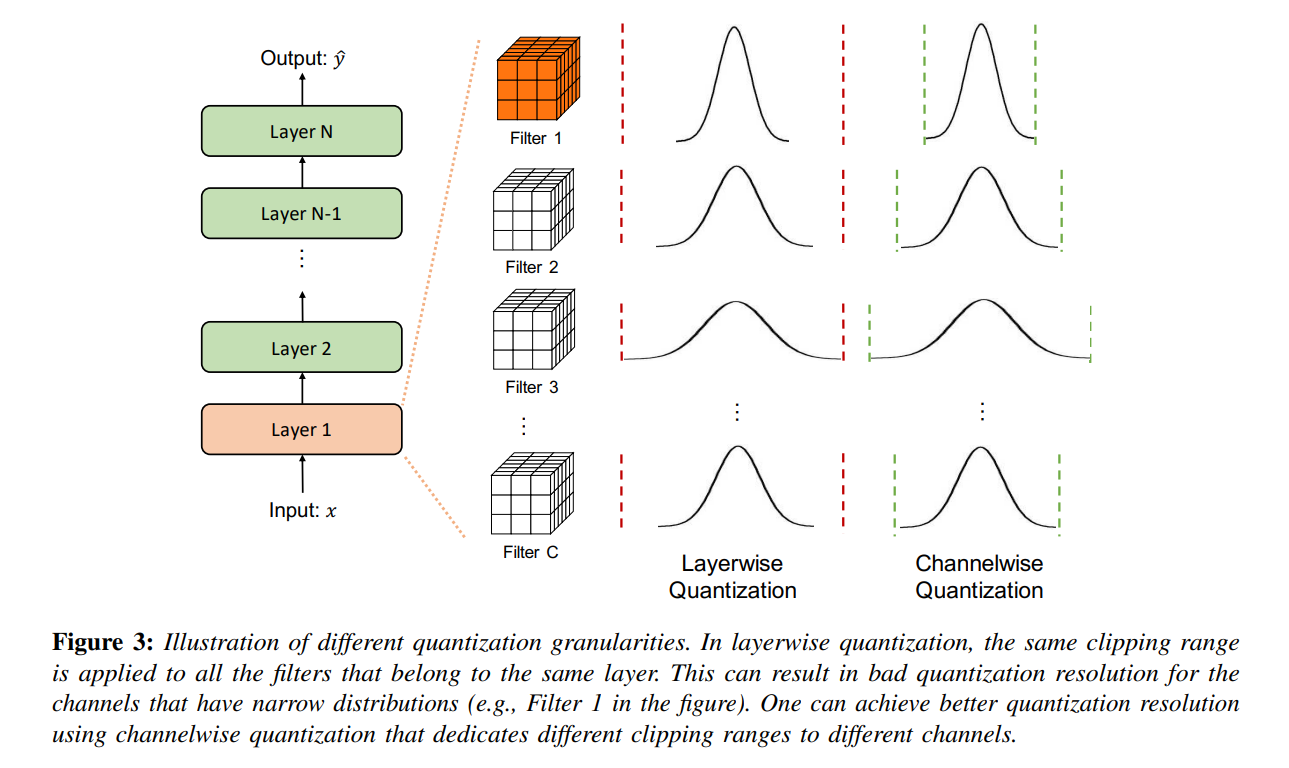
Layer-wise Quantization은 layer마다 convolutional filter에 있는 모든 파라미터를 고려해서 $\alpha, \beta$를 결정한다. 그래서 하나의 layer에 있는 filter들은 동일한 범위로 quantization이 진행된다. 이 방법은 구현하기 간단하지만 종종 정확도측면에서 손실이 발생한다. 왜냐하면 layer 안에서도 필터마다 값의 범위가 다양하기 때문이다. Figure 3을 보면 Layer 1에 있는 Filter 4개의 분포가 모두 상이하다. 하지만 Layer Quantization은 모든 필터에 같은 clipping range를 적용하기 때문에, resolution이 좋지 않은 Filter가 발생한다. (위의 그림에서 Filter 1, Filter 2, Filter C 의 경우 resolution이 좋지 않다.)

Group-wise Quantization은 layer 안에서도 필터끼리 묶어서 서로 다른 $\alpha, \beta$를 설정한다. 이 방법은 하나의 convolution/activation마다 파라미터의 분포가 상이하게 다른경우에 도움이 된다. 예를들어 Q-BERT 같은 모델에서 이 방법을 사용해서 성능이 2%정도 감소하고 파라미터를 13배나 압축하는 결과를 얻었다.

Channel-wise Quantization은 각 filter마다 clipping range를 설정하는 방법이다. 이 방법은 quantization resolution이 좋고 종종 accuracy 측면에서 성능이 좋다. 현재 convolution kernel을 quantization할 때 가장 많이 사용하는 방법이다. Figure 3에 오른쪽 그림을 보면, channel마다 clipping range가 다르다.

Sub-channel-wise Quantization은 convolution filter 하나에서도 group을 나누어서 clipping range를 설정하는 방법이다. Resolution은 좋아지지만 계산량이 많아져서 잘 쓰이지 않는다.

2.5. Non-Uniform Quantization

Uniform quantization은 $[\alpha, \beta]$에서 균일한 간격으로 같은 값으로 quantization을 진행헀다. 하지만 간격 크기를 다르게하고, 간격마다 다른 값으로 quantization 하는 기법이 non-uniform quantization이다. 일반적으로 다음과 같이 표현한다.

\[Q(r)=X_i \text {, if } r \in\left[\Delta_i, \Delta_{i+1}\right) \tag{3}\]

$X_i$는 quantization level, $\left[\Delta_i, \Delta_{i+1}\right)$는 quantization steps이다. 각 구간마다 다른 level로 quantization이 진행되고 구간마다 길이가 다르다. 이 방법은 fixed bit-width일 때 좋은 성능을 얻을 수 있다. 왜냐하면 중요한 값이 많이 몰려있는 영역에 집중해서 resolution을 높이고, 중요하지 않은 영역의 resolution은 낮추면 되기 때문이다. 예를들어 non-uniform quantization은 대부분 파라미터 값의 분포를 bell-shape로 설정한다. 최근 기법들은 quantizer Q를 학습을 통해 찾아낸다.

\[\min _Q\|Q(r)-r\|^2 \tag{4}\]

위의 최적화 문제를 풀어서 quantizer를 구한다. 위의 방법 외에도 clustering 방법을 사용해서 파라미터마다 quantizer를 구하는 방법도 있다.

non-uniform quantization은 uniform에 비해 더 많은 정보를 표현할 수 있지만, GPU 혹은 CPU에서 효율적으로 연산을 하기 어어려워서 대부분 uniform quantization을 사용한다.

2.6. Fine-tuning Methods

Quantization 이후에 네트워크의 파라미터 조정이 필요한 경우가 있다. 이런 경우에 모델을 다시 학습하는 Quantization-Aware Training (QAT) 방법이 있고, 모델을 다시 학습하지 않는 Post-Training Quantization (PTQ)가 있다.

2.6.1. Quantization-Aware Training (QAT)

Quantization을 적용하면 모델 파라미터에 perturbation을 가한 것이기 때문에 floating point precision으로 학습했을 때 수렴했던 곳과 다른 곳에 위치하게 된다. 그래서 quantized model을 다시 학습해서 loss를 수렴시킬 필요가 있다. QAT는 이런 문제를 해결해주는 방법인데, Quantized weight를 사용해서 forward, backward pass를 한 후에 얻어진 quantized gradient를 floating point로 변환한 후에 gradient를 update한다. 정리하자면 다음 그림과 같다.

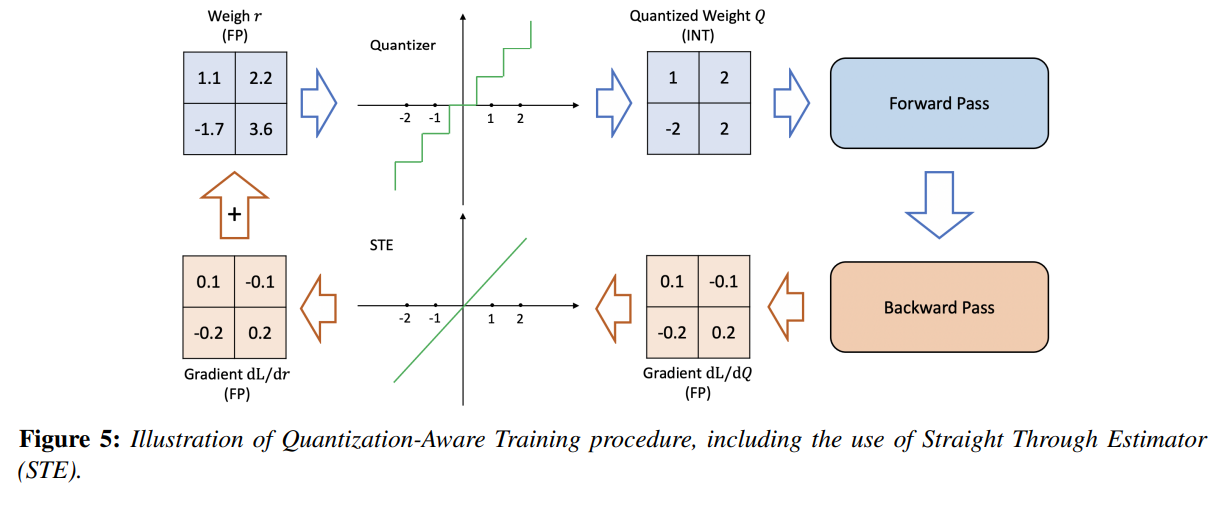
위에서 $\frac{dL}{dQ}$를 $\frac{dL}{dR}$로 변환할 때, Straight Through Estimator (STE)를 사용하는데, STE는 quantized gradient로 real gradient를 근사하는 기법이다. 실제로 Binary Quantization 처럼 너무 낮은 precision quantization 기법을 제외하고, STE 근사 성능이 좋다. STE 이외에도 gradient를 근사하는 기법이 연구되고있다.

Gradient 근사 기법외에도 다른 방식으로 QAT를 하는 방법이 있는데, ProxQuant라는 방법은 (1)에서 사용된 rounding operation을 없애고, 파라미터에 non-smooth regularization(W-shape)을 적용해서 quantized value를 얻는 기법을 사용한다. 또 다른 방법으로는 pulse training이 있는데, 이 방법은 불연속점의 derivative를 근사하거나, quantized weight를 floating point와 quantized parameter의 affine combination으로 바꿔서 QAT를 진행한다. 하지만 이런 기법들은 tuning이 많이 필요해서 STE가 일반적으로 많이 사용된다.

모델 파라미터를 조정하는 방법 외에도, QAT를 하는 과정중에 quantization parameter를 학습하는 방법이 있다. PACT는 clipping range를 학습하는 방법이고, QIT는 quantization step을 학습한다.

QAT는 효과가 좋지만 모델을 다시 학습해야한다는 추가적인 비용이 발생한다. Quantized model이 오랜 기간동안 deploy된다면 QAT를 적용할만하지만, 모델의 라이프사이클이 짧은 경우, QAT가 시간낭비가 될 수 있다.

2.6.2. Post-Training Quantization (PTQ)

Fine-tuning 없이 quantization을 수행하고 weight를 조정하는 방법이다. PTQ는 QAT에 비해 오버헤드가 거의 없고, re-training을 할 때 많은 양의 데이터가 필요하지 않고, unlabeled data에 대해서도 적용이 가능하다. 하지만 QAT에 비해 accuracy는 낮아진다. 그래서 lower accuracy를 개선하려고 여러가지 방법이 연구되고 있다. 대표적으로 OMSE는 quantized tensor와 floating point tensor 사이에 L2 distance를 줄이는 방향으로 학습을 진행한다.

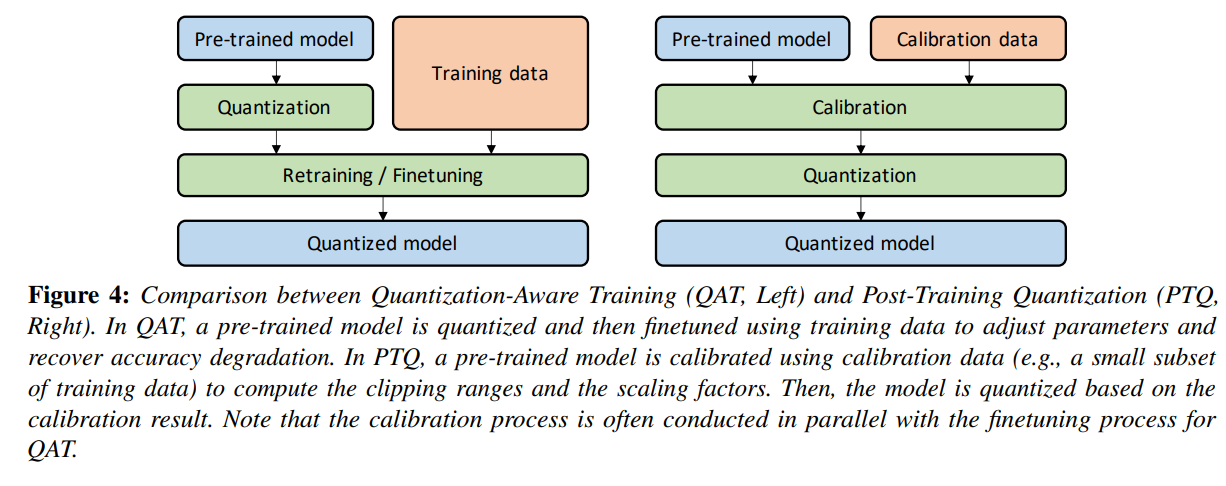
위의 그림은 QAT와 PTQ를 비교한 것이다. 둘의 차이점은 QAT는 학습 데이터 전체가 fine-tuning 과정에서 사용되고, PTQ는 일부 데이터만 Calibration 과정에서 사용이 된다는 점이다.

2.6.3. Zero-shot Quantization (ZSQ)

앞선 방법들은 quantization 과정에서 학습데이터를 사용했는데, 학습 데이터가 너무 커서 분산되어있거나, 보안같은 문제로 학습 데이터를 이용하지 못하는 경우가 있다. 이 경우에 zero-shot quantization을 사용할 수 있는데, 두 가지 수준으로 나누어진다.

• Level 1: No data and No fine-tuning (ZSQ + PTQ)
• Level 2: No data but requires fine-tuning (ZSQ + QAT)

Level 1 방법은 weight 범위를 동일하게 맞춰주거나, bias error를 수정하는 방식으로 이루어진다. 이 방법은 linear activation의 scale-equivariance property에 근거한 방법이기 때문에, non-linear activation의 경우 sub-optimal solution을 얻을 가능성이 있다.

ZSQ 연구방향중 유명한 갈래 중 하나인 synthetic data를 생성하는 방법이 있다. Pre-trained model을 discriminator로 삼고, 학습 데이터와 유사한 synthetic data를 생성해서 quantization model을 fine-tuning하는 방법이다. 하지만 이 방법은 internal statistics ( distributions of the intermediate layer activations)을 고려하지 않은 방법이기 때문에 실제 데이터 분포를 잘 나타내지 못한다. 그래서 batch normalization에 저장된 statistics를 이용해서 더 실제같은 synthetic data를 생성하는 방법도 있다. 실제 데이터 분포와 유사한 synthetic data를 만들어낼 수록, ZSQ 성능이 좋다는 연구결과들이 있다.

2.7. Stochastic Quantization

Quantization 과정에서 Stochastic 성질을 주면 rounding operation으로 인해서 weight 변화가 없을 거라는 생각을 할 수 있지만, stochastic rounding을 통해 네트워크는 탈출(?)할 수 있게 돼서 파라미터 업데이트가 가능하다. 예를들어 다음과 같은 방식으로 Stochastic Rounding 적용이 가능하다.

\[\operatorname{Int}(x)= \begin{cases}\lfloor x\rfloor & \text { with probability }\lceil x\rceil-x \\ \lceil x\rceil & \text { with probability } x-\lfloor x\rfloor\end{cases} \tag{5}\]

Binary Quantization의 경우는 다음과 같이 사용이 가능하다.

\[\operatorname{Int}(x)= \begin{cases}\lfloor x\rfloor & \text { with probability }\lceil x\rceil-x \\ \lceil x\rceil & \text { with probability } x-\lfloor x\rfloor\end{cases} \tag{6}\]

최근에는 QuantNoise가 computer vision이나 NLP에서 accuracy 변화가 거의 없이 quantization을 사용했다. 이 방법은 forward pass할 때 마다 임의의 weight subset을 quantize하고 unbiasd gradient로 모델을 학습시키는 방법이다. 하지만 이 방법의 단점은 weight를 update할 때마다 random number를 생성해야하는 오버헤드가 있다는 점이다. 이 때문에 실제로 거의 사용되지 않는다.

3. Quantization Below 8 Bits

3.1. Simulated and Integer-only Quantization

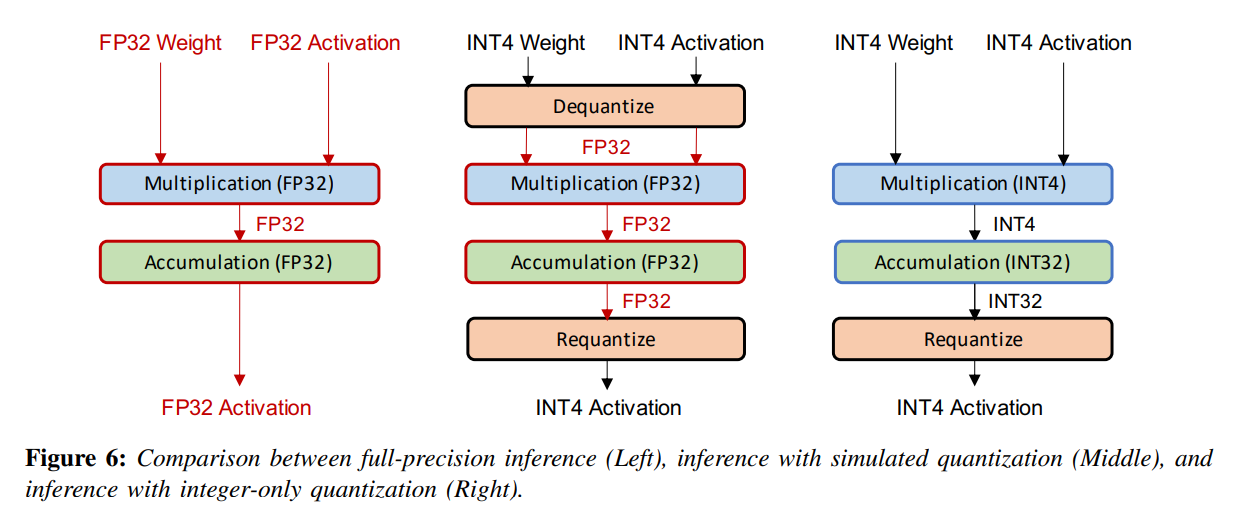
Quantized model을 배포하는 두 가지 방법이있다. 첫번째는 simulated quantization (fake quantization)인데, 이 방법은 quantized model parameter를 lower-precision으로 저장을 하지만 행렬곱이나 컨볼루션같은 연산을 floating point로 수행한다. 그래서 quantized parameter는 floating point 연산을 하기 전에 dequantized 되어야한다. 그래서 빠르게 연산을 할 수 없다는 단점이 있다.

(저장할 때 용량을 줄이기 위해서 이렇게 하는건가?)

두번째는 Integer-only quantization이 있는데, 이 방법은 모든 연산이 low-precision integer에서 수행이 돼서 속도가 빠르다. low-precision에서는 latency, power consumption, area efficiency 측면에서 full-precision보다 좋다. 많은 hardware processor들이 기본적으로 빠른 low-precision 연산을 지원한다. 또한, Int 8 덧셈 연산이 FP32 덧셈 연산보다 에너지 관점에서 30배 좋고, area 관점에서 116배 좋다.

Dyadic quantization은 integer-only quantization의 한 종류인데, dyadic number(분자가 정수, 분모가 2의 거듭제곱)를 사용해서 모든 scale 연산이 수행된다. 이 방법을 사용하면 나눗셈 없이, integer 덧셈, 곱셈, 비트이동 만으로 모든 연산을 나타낼 수 있다.

Integer-only quantization은 속도 측면에서 fake quantization보다 좋다. 하지만 추천시스템처럼 compute-bound보다 bandwidth-bound 문제가 되는 경우에 fake quantization이 효과적이다. 왜냐하면 이런 경우 대부분 병목현상이 메모리 사용량과 파라미터를 메모리에서 로드하는데서 발생하기 때문이다.

셋을 정리하자면 다음과 같다.

	Full Precision	Simulated Quantization	Integer-only Quantization
저장	FP32	INT 4	INT 4
연산	FP 32	FP 32	INT 4
출력	FP 32	INT 4	INT 4

3.2. Mixed-Precision Quantization

이 방법은 각 layer를 다른 bit precision으로 quantized하는 방법이다. 이때 결정하는 기준은 각 layer의 quantization에 대한 sensitivity이다. 만약 어떤 layer에 quantization을 적용했을 때 성능 저하가 심하면 (sensitivity가 크면) 해당 layer 파라미터는 higher bit precision으로 quantization을 적용하고, 반대로 어떤 layer에 quantization을 적용했을 때 성능에 변화가 거의 없다면, lower precision bit를 사용하는 기법이다. 이 방법의 단점은 layer 수가 많아질 수록 각 layer 마다 bit를 결정하기 위해 탐색 범위가 지수적으로 증가한다는 점이다. 그래서 탐색 범위를 제한하기 위한 방법들이 제안되고 있다.

최근 논문은 강화학습 (RL) 기반으로 quantization policy를 결정하는 방법을 제시한다. Hardware simulator를 agent로 설정해서, hardware 가속이 얼마나 되는지를 기준으로 policy를 결정한다. 다른 논문은 search space 문제를 Neural Architecture Search (NAS) 문제로 간주해서 search space를 찾는다. 이런 방법들은 계산량이 많이 필요하고 초기 변수값과 하이퍼파라미터에 민감하다는 단점이 있다.

다른 방법으로는 HAWQ가 있는데, 이 방법은 각 layer에 quantization을 적용했을 때 Hessian matrix를 통해 sensitivity를 측정해서 bit precision을 결정한다. 이 방법은 Pruning에서 중요한 논문 중 하나인 Optimal Brain Damage와 유사하다. HAWQv2에서는 layer의 파라미터 뿐만 아니라 activation까지 quantization을 적용했는데, RL 기반 mixed-precision보다 100배나 빠른 결과가 나타났다. HAWQv3는 integer-only, hardware-aware quantization 방법이 도입되었다. 이 방법은 Integer Linear Programming을 사용해서 optimal bit precision을 결정한다. T4 GPU를 기준으로 mixed-precision (INT4/INT8) quantization을 사용했을 때 INT8 quantization보다 속도가 50배나 향상되었다.

3.3. Hardware Aware Quantization

Quantization의 목표 중 하나는 inference latency를 줄이는 것이다. 하지만 quantization을 적용했다고 해서 모든 hardware가 동일하게 inference 속도를 향상시키는 건 아니라, hardware의 on-chip memory, bandwidth, cache hierarchy에 따라 결정된다. 그래서 hardware-aware quantization 방법이 연구되고 있다.

3.4. Distillation-Assisted Quantization

Accuracy가 높은 large model에서 생성한 output을 이용해서 quantization을 진행하는 방법이 있다. 이때 어느 부분의 output을 이용하는지에 따라 방법이 나뉘는데, 마지막 layer의 soft probabilities를 사용하거나, 중간 layer의 feature를 사용하는 방법이 있다. Teacher model과 Student model을 각각 생성하는 방법도 있지만, 추가적인 teacher model 없이 self-distillation하는 방법도 있다.

3.5. Extreme Quantization

Quantization의 가장 극단적인 경우는 1-bit representation (Binarization)이다. 이 방법은 memory 사용량을 32배 줄여줄 뿐만 아니라, bit-wise arithmetic을 사용해서 binary (1-bit) and ternary (2-bit) 연산을 가속할 수 있다. 예를들어 NVIDIA V100 GPU에서 peak binary arithmetic은 INT8보다 8배 빠르다. 하지만 단순히 binarization을 적용하면 accuracy 감소현상이 심하기 때문에 binarization을 잘하는 방법을 연구하고있다.

BinaryConnect는 파라미터를 실수값으로 저장하는데, forward와 backward pass를 할 때만 sign값을 기준으로 +1과 -1을 할당해서 연산을 한다. Sign 함수가 미분 불가능하기 때문에 STE estimator를 사용해서 gradient를 근사한다. Binarized NN은 파라미터 뿐만아니라 activation까지도 binarization을 적용하는 방법이다. 이를 통해 latency를 낮추었다. Binary Weight Network (BWN)은 scale factor를 추가해서 $+\alpha, -\alpha$로 binarization을 수행하는 방법이다. 이때 $\alpha$를 결정할 떄 다음과 같은 최적화 문제를 푼다.

\[\alpha, B=\operatorname{argmin}\|W-\alpha B\|^2 \tag{7}\]

위의 방법으로 학습한 weight가 0에 가깝다는 관찰을 바탕으로, binarization 대신 tenarization (+1, 0, -1)을 적용하는 방법도 있다. 이 방법은 binarization보다 행렬곱 연산속도를 줄여주기 때문에 inference latency가 감소한다.

최근에는 BERT, RoBERTa, GPT같은 pre-trained model에 extreme quantization을 적용하는 방법들이 연구되고 있다.

Binarization과 Tenarization을 단순히 적용하면 accuracy 감소가 심하기 때문에 ImageNet 분류처럼 복잡한 테스크에서 성능이 좋지 않다. 그래서 이 문제를 해결하려고 3가지 방향으로 연구가 진행되고 있다.

• Quantization Error Minimization

이 방법은 weight의 실수값과 quantized value 차이를 최소화하는 것을 목표로 한다. real-value weight/activation을 단일 binary matrix로 표현하는 대신, binary matrix의 선형 결합( 식 )으로 표현해서 quantization error를 줄인다.

• Improved Loss Function

이 방법은 Binarized/ternatized weight에 대해서 loss를 직접 최소화 하는 방법이다. 다른 방법들은 quantized weight가 loss function에 반영되지 않는데, 이 방법은 반영이 된다.

• Improved Training Method

Sign함수의 gradient를 근사할 때 STE를 사용하는데, STE는 [-1, 1] 사이에 gradient만 전파가능하다는 단점이 있다. 그래서 BNN+에서는 sign 함수의 미분을 연속함수로 근사하는 방법을 도입했고, 다른 방법에서도 sign 함수를 smooth하고 미분가능한 함수로 대체하는 방법을 사용했다.

3.6. Vector Quantization

디지털 신호 처리 (DSP)에서 역사적으로 quantization과 관련된 연구가 많이 진행됬는데, ML에서 quantization과 접근 방법이 조금 다르다. DSP에서는 신호를 최대한 오류없이 압축하는 방법에 관심이 있는데, ML에서는 파라미터나 activation을 reduced-precision으로 표현하는데 관심이 있기 때문이다.

그래도 DSP에서 사용하는 quantization 방법을 ML에 적용하려는 시도들이 있었다. 특히 clustering 방법이 많이 연구 됐는데, weight를 비슷한 값끼리 clustering해서 몇 개의 그룹으로 나눠서 얻은 중심점을 quantized value로 사용하는 방법이다. 실제로 K-means clustering을 사용해서 급격한 accuracy 감소없이 8배나 모델 사이즈를 줄인 성과가 있었다. 게다가 pruning과 Huffman coding을 같이 적용해서 모델 크기를 더 줄이는 연구도 있었다.

Product Quantization은 weight matrix를 sub-matrices로 나누고, 각 sub-matrix에 vector quantization을 적용하는 방법이다.

4. Future Directions for Research in Quantization

4.1. Quantization Software

정확성을 잃지않고 INT8 quantization 모델로 배포할 수 있는 소프트웨어 패키지들이 많이 있다. 하지만 lower bit-precision quantization에 관한 소프트웨어는 많이 없다.

4.2. Hardware and NN Architecture Co-Design

NN architecture의 width를 변화시키면 quantization 이후에 generalization gap이 줄어든다는 연구 결과가 있다. 그래서 Quantization을 할 때 depth나 kernel 처럼 architecture 구조 파라미터도 같이 학습하는 방법이 연구되고 있다.

또는 hardware architecture와 같이 quantization method를 설계하는 연구도 있다. 예를들어 FPGA에서 배포를 할 때 이런 방식으로 설계하면 효과가 좋을 거라 예상한다.

4.3. Coupled Compression Methods

Quantization이 다른 방법과 같이 사용될 수 있는데, 어느 경우에 최적의 조합이 되는지에 관한 연구가 거의 없다.

4.4. Quantized Training

Quantization을 학습과정에 적용할 수도 있는데, INT8 precision training을 적용하려면 어려움이 많다고 한다. 보통 하이퍼 파라미터 튜닝이 많이 필요하거나 상대적으로 쉬운 task에만 적용이 된다고 한다. 왜냐하면 INT8 precision을 사용해서 학습을 하면, 학습이 불안정하고 발산할 수 있기 때문이다.

Summary

• Quantization은 weight와 activation에 적용이 가능하다.