Motivation
기존 논문들은 activation quantization 영향을 고려하지 않은 채 weight quantization을 이론적으로 분석하였습니다. 본 논문에서는 PTQ block reconstruction 단계에서 activation quantization의 영향을 이론적으로 분석하였습니다. 논문의 결론은 reconstruction 과정에서 일부 activation에 대해서 quantization을 진행하면 flatness of model on calibration data 가 증가해서 test data에 대해 flatness가 증가한다고 합니다. 여기서 flatness는 특정 parameter에 perturbation을 적용했을 때 loss 값이 변화하는 정도를 의미합니다. 수식으로는 다음과 같습니다.
Keyword
- flatness
- $u(x)$: activation perturbation / $v(x)$: weight perturbation
Proposed Method
먼저 논문에서 reconstruction 과정에서 activation quantization의 영향을 파악하기 위한 실험을 진행합니다.

3가지 경우에 대해 비교 실험을 진행합니다.
Case 1: weight only quantization
Case 2: weight + activation quantization
Case 3: weight + activation (1~k-1 th block) / weight quantization (k th block)
Table 1을 보시면 low-bit 상황에서 3번 case 성능이 꾸준히 좋다는 것을 볼 수 있습니다. 1, 2번을 비교하면 PTQ reconstruction 과정에서 activation을 고려하면 성능이 많이 증가한다는 것을 관찰할 수 있습니다. 2, 3번을 비교하면 부분적으로 activation을 고려하면 성능이 향상된다는 것을 알 수 있습니다.
본 논문에서는 이런 실험 결과가 나타난 이유를 이론적으로 분석했습니다. 먼저 weight과 activation에 quantization을 적용했을 때 발생하는 오류를 다음과 같이 나타냅니다.
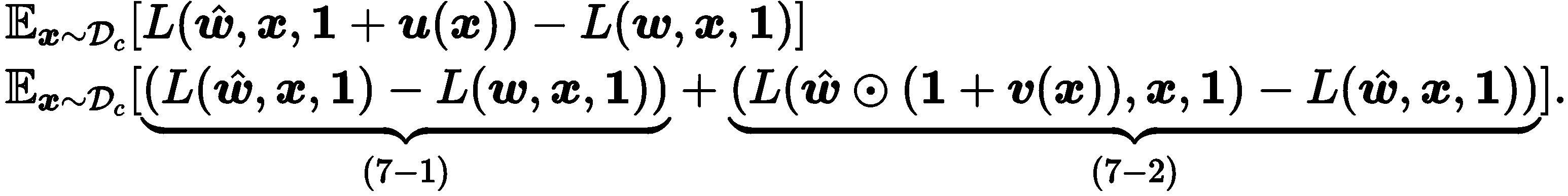
(7-1) 은 weight quantization을 적용했을 때 발생하는 quantization error이고, (7-2)는 activation quantization을 적용했을 때 발생하는 quantization error입니다. 저자는 calibration data로 학습한 weight perturbation과 activation perturbation이 test data에 대해서도 loss를 낮추는 방향으로 이어지는지 확인하기 위해 (7-1), (7-2) 각 term을 test data에 대해서 분석합니다.
먼저 test data에 대한 (7-1) term을 살펴보겠습니다. Calibration data에 대해서 (7-1) term만 낮추는 방향으로 PTQ를 하면 calibration data에 대한 weight quantization error를 낮추는 방향으로 학습하게 돼서, test data에 대한 weight quantization error는 증가할 가능성이 있습니다. 그래서 calibration data에 대해서 (7-2) term 까지 같이 고려해서 PTQ를 하게 되면 calibration data에 대한 weight quantization error를 낮추면서 동시에 calibration data에 대한 flatness를 증가하는 방향으로 PTQ가 진행되므로, test data에 대한 weight quantization error가 줄어들게 됩니다. 왜냐하면 Figure 2에서 (완전히 겹치지는 않지만) calibration data와 test data의 flatness 경향이 각 case 별로 비슷하기 때문입니다. 마찬가지로 test data에 대한 (7-2) term은 test data에 대한 flatness를 의미하는데, Figure 2에서 calibration data와 test data flatness 경향이 유사하므로 calibration data에 대해서 (7-2) term을 낮추는 방향이 곧 test data에 대해서 flatness를 높이는 방향으로 이어진다고 주장합니다.
하지만 Fig. 2에서 두 데이터에 대한 flatness 경향이 비슷하긴 하지만 완전히 일치하지는 않으므로, Case2 처럼 무조건 activation quantization을 적용해서 calibration data에 대한 flatness를 증가하는 방향으로 PTQ를 진행하게 되면 calibration data에 overfitting 가능성이 커지게 됩니다. 그래서 저자는 dropout 처럼 calibration data 일부에 대해서만 activation quantization을 진행해서 calibration data에 overfitting 되는 것을 방지해서 다음과 같은 식을 activation quantization에 사용했습니다.

위 식을 기반으로 확률에 따라 activation perturbation $u(x)$를 조절해서 flatness를 높이는 동시에 calibration data에 overfitting 되는 것을 방지하게 됩니다.

위 그림은 ResNet-18에서 각 경우마다 test data에 대해서 quantized weight의 loss surface를 그린 그래프인데, QDrop의 경우에 그래프가 가장 평평하다는 것을 알 수 있습니다.

실제로 적용되는 알고리즘을 살펴보면, $k$번째 block에 layer index가 $[i, j]$일 때, $j$번째 layer까지 forward pass를 하면서 각 layer마다 랜덤하게 activation을 quantize합니다. 그렇게 block의 마지막 layer의 randomly quantized activation과 original activation의 차이를 구하고, 해당 값을 기준으로 BRECQ에서 했던 것처럼 quantized weight과 activation scale을 학습합니다.
Experiment
Setting
- Set 8-bit in the first and the last layer (except NLP task)
- Per-channel weight quantization
QDROP을 적용했을 때 Classification, Detection, NLP task에서 BRECQ에 비해 성능 향상이 있다는 것을 실험적으로 증명합니다. 또한 cross-domain (calibration: MS COCO, CIFAR100 → test: ImageNet) 상황에서도 QDROP이 효과가 있다는 걸 실험적으로 보여줍니다.
Discussion
비교적 간단한 방법으로 calibration data와 test data 사이의 간극을 줄일 수 있다는 점에서 의미가 있어 보입니다. 아쉬운 점은 bit가 작은 상황 (2~4)에 대해서만 실험을 해서 자주 사용하는 Weight: 8 / Activation: 8 bit setting에 대한 실험이 없다는 점입니다.
Comments powered by Disqus.