Recent Advances on Neural Network Pruning at Initialization 정리

1. Introduction

기존의 Pruning 기법은 pretrained model에 적용하는 방법이 대부분이었습니다. 하지만 최근에는 임의로 초기화된 네트워크 (a randomly initialized network)에 pruning 기법을 적용하는 방법들이 연구되고 있습니다. 이 기법을 Pruning at Initialization (PaI) 라고 하는데, 이 논문에서는 PaI 기법들에 대해 정리하고 있습니다.

보통 Pruning pipeline은 3단계로 이루어져 있습니다.

(1) Pre-training a dense model.

(2) Pruning the dense model to a sparse one.

(3) Fine-tuning the sparse model to regain performance.

이처럼 Pruning은 pre-trained dense model에 적용하는 post-processing 기법 (Pruning after Training, PaT) 이었는데, 최근에는 임의로 초기화된 네트워크에 적용되는 기법 (PaI)이 연구되고 있습니다. 이전에는 Sparse network를 처음부터 학습했을 때 성능이 안 좋았다는 연구가 많았는데, 최근에는 lottery ticket hypothesis (LTH)와 SNIP 논문에서 sparse network를 처음부터 학습시켰을 때, 원래 network와 성능이 유사했다는 연구결과가 발표되었습니다. 이 논문 이후로 처음부터 sparse network를 학습시키는 방법이 연구되고 있습니다.

2. Background of Neural Network Pruning

2.1. Classic Topics in Pruning

어떤 모델에 Pruning을 적용할 때 중요한 4가지 질문이 있습니다. 어떤 구조로 pruning 할건지, 얼마나 pruning 할건지, 어떤 기준으로 pruning을 할건지, 마지막으로 pruning 과정을 어떻게 스케쥴링할 것인지 입니다. 이거에 대해서는 여기서 간단히만 다루고, 자세한 내용은 이 논문을 참조하시면 됩니다.

2.1.1. Sparsity Structure

Pruning을 특정 pattern에 따라 적용하는 Unstructured Pruning이 있고, pattern을 신경쓰지 않고 단일 weight에 적용하는 Structured Pruning이 있습니다. Structured Pruning은 channel, filter, block 등 특정 단위로 적용하는 방법입니다.

Unstructured Pruning은 주로 model size 압축에 사용이 되고, Structured Pruning은 모델 가속에 사용이 됩니다. 왜냐하면 Structured Pruning을 통해 weight을 block 단위로 메모리에 하드웨어에 맞게 저장해서 속도를 빠르게 할 수 있습니다.

2.1.2. Pruning Ratio

Pruning Ratio는 얼마나 많은 weight를 제거할지 결정하는 값입니다. 일반적으로 ratio를 결정하는 방법이 두가지가 있습니다.

미리 정의하는 방법

모든 layer를 하나의 ratio 값으로 pruning 하는 방법이 있고, layer 마다 ratio를 다르게 주는 방법이 있습니다.

다른 방법을 통해 결정하는 방법

Regularization 같은 방법을 통해 간접적으로 pruning ratio를 결정할 수 있습니다.

하지만 특정 Sparsity에 도달하기 위해서 ratio를 얼마나 설정해야할지 결정하기 위해서는 많은 tuning 과정이 필요합니다. 그리고 미리 정의하는게 좋은지, 자동으로 찾는게 좋은지에 관해서도 의견이 분분해서 아직까지 합의점은 찾지 못했습니다.

2.1.3. Pruning Criterion

Pruning criterion은 어떤 기준으로 weight을 제거할지 결정합니다. 이 문제는 pruning에서 가장 중요해서 많은 Pruning 연구들이 criterion 중심으로 진행되고 있습니다. 가장 단순한 방법으로는 weighted magnitude ( $L_1$-norm for a tensor)를 기준으로 제거하는 것인데, 이 방법이 간단해서 PaT에서 많이 사용되고 있습니다. 대부분 Criterion 설계방식은 특정 weight를 제거했을 때 loss 변화가 가장 적은 파라미터를 선택하는 걸 중점적으로 생각합니다.

Criterion 관련해서 많은 연구가 진행됐지만, 어떤 방법이 다른 방법보다 확실하게 낫다고 말하기가 어렵습니다. 이에 관해서는 PaT 논문에서 많이 논의가 되었기 때문에 여기서는 넘어가도록 하겠습니다.

2.1.4. Pruning Schedule

위에 3가지가 결정된 후에 pruning scheduling 방법을 결정하는데, 세가지 종류가 있습니다.

(1) One-shot: 단일 스텝으로 한번에 ratio만큼 pruning을 진행하고, fine-tuning을 하는 방법입니다.

(2) Progressive: 점진적으로 network sparsity를 0에서 ratio만큼 증가시키고, fine-tuning을 적용하는 방법입니다.

(3) Iterative: Network sparsity를 0에서 ratio의 중간지점까지 만든 후에 fine-tuning을 하고, 그 후에 Network sparsity를 중간지점에서 target ratio까지 만든 후에 다시 fine-tuning을 적용하는 방법입니다.

보통 (2)와 (3)을 pruning interleaved with network training이라고 부르는데, 두 개사이에 기본적인 차이점을 없어서 어떤 논문에서는 progressive와 iterative를 같은 의미로 사용합니다.

그리고 같은 수의 weight을 pruning 할 때, (2)와 (3)이 one-shot보다 성능이 좋다는 것을 대부분 동의합니다. 왜냐하면 (2)와 (3)이 더 많은 iteration을 필요로하기 때문입니다.

2.2. A generic Formulation of Pruning

먼저 Pruning Paradigm을 수학적으로 정의하고, 그 정의를 바탕으로 PaT와 PaI를 비교하겠습니다. 파라미터가 $\mathbf{w}$인 neural network를 학습시킬 때 $K$번째 iteration에 모델이 수렴한다고 가정하면, 파라미터 시퀀스를 다음과 같이 나타낼 수 있습니다.

\[\{\mathbf{w}^{(0)},\mathbf{w}^{(1)}, ..., \mathbf{w}^{(i)}, ..., \mathbf{w}^{(K)}\}\]

Sparse network에서는 sparse 구조를 mask로 표현이 가능합니다. 특정 dataset $\mathcal{D}$를 갖고 Pruning을 수행한다고 하면, 마스크를 다음과 같은 함수로 나타낼 수 있습니다.

\[\mathbf{m} = \mathbf{f_1}(\mathbf{w}^{(k_1)};\mathcal{D})\]

그리고 pruning 하는 과정에서 기존 파라미터가 조금 변할 수 있는데, 그걸 다음과 같은 함수로 나타낼 수 있습니다.

\[\mathbf{f_2}(\mathbf{w}^{(k_2)};\mathcal{D})\]

마지막으로 pruning을 하고 나서 원래 모델의 performance와 성능을 유사하게 만들기 위해서 fine-tuning 과정을 하는데, 그 과정을 다음과 같은 함수로 표현이 가능합니다.

\[\mathbf{f_3}(\mathbf{w}';\mathcal{D})\]

위에 식 3개를 합쳐서 Pruning의 전체 과정을 다음과 같이 나타냅니다.

\[\begin{aligned}\mathbf{w}^{\prime} & =\mathbf{f}_{\mathbf{1}}\left(\mathbf{w}^{\left(k_1\right)} ; \mathcal{D}\right) \odot \mathbf{f}_{\mathbf{2}}\left(\mathbf{w}^{\left(k_2\right)} ; \mathcal{D}\right), \\\mathbf{w}^* & =\mathbf{f}_{\mathbf{3}}\left(\mathbf{w}^{\prime} ; \mathcal{D}\right)\end{aligned}\]

마지막에 얻어진 $\mathbf{w}^*$ 값이 최종적인 pruned model이고, $\mathbf{f_1}$과 $\mathbf{f_2}$가 다른 iteration $k_1, k_2$를 사용할 수 있다는 점을 주목해야 합니다. PaI는 Sparse Training과 Sparse Selection 기법으로 나누어지는데, 위에 정의를 바탕으로 PaT, Sparse Training, Sparse Selection을 구분하면 다음과 같습니다.

Pruning after Training (PaT): $k_1 = K, k_2 = K$
Sparse Training (PaI): $k_1 = K$ (LTH) or 0 (SNIP), $k_2 = 0 \,\,;\, \mathbf{f_2}=\mathbf{I}$ (identity function), $\, \mathbf{f_3} \neq \mathbf{I}$
Sparse Selection (PaI): $k_1=k_2=0$, and $\mathbf{f_2}=\mathbf{f_3}=\mathbf{I}$

위에 나온대로 PaT는 초기 모델이 pre-training 과정을 거쳐서 수렴했을 때 (K번째 iteration) 얻은 mask와 weight를 그대로 사용해서 fine-tuning 과정을 거쳐서 pruning을 수행합니다.

PaI 중에서 Sparse Training은 LTH와 SNIP으로 나누어지는데, LTH에서는 pre-training에서 얻은 mask를 사용하지만 weight는 pre-training 이전 초기값을 사용하고, SNIP에서는 mask와 weight 모두 초기값을 사용합니다. 이후에 추가적으로 $\mathbf{f_3}$에서 fine-tuning 과정을 적용하는 게 Sparse Training의 특징입니다. Sparse Selection은 mask와 weight 모두 초기값을 사용하고, fine-tuning도 하지 않습니다.

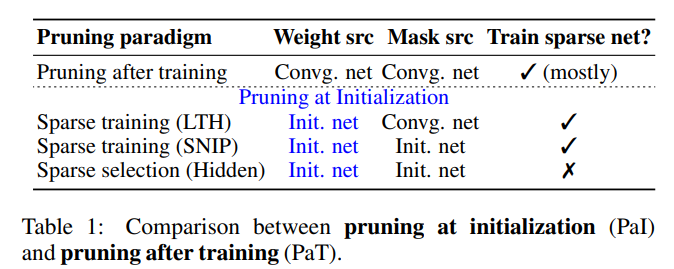
지금까지 말한 내용을 정리하면, PaI와 PaT를 구분하는 기준은 수렴한 network의 weight를 그대로 사용할지 아니면 초기화할지 여부이고, Sparse Training과 Sparse Selection을 구분하는 기준은 fine-tuning 유무입니다. 이를 표로 정리하면 다음과 같습니다.

이제 LTH와 SNIP에 대해 간단히 살펴보고, Sparse Training과 Sparse Selection에 대해서 자세히 소개하겠습니다.

3. Pruning at Initialization (PaI)

3.1. Overview: History Sketch

LTH and SNIP

PaI가 주목받게된 이유는 PaT에서 필요한 pre-training과 복잡한 pruning schedule이 필요 없어서 pruning을 더 적은 계산비용으로 간단하게 수행할 수 있기 때문입니다. 기존에는 임의로 초기화된 sparse network를 dense network와 같은 성능으로 학습할 수 없다는 결과가 많았는데, LTH와 SNIP 두 논문에서 sparse network로도 dense network만큼 충분히 좋은 성능을 낼 수 있다는 것을 보여주었습니다. 두 방법의 차이점은 LTH는 pre-trained model에서 mask를 얻는다는 점이고 (post-selected mask), SNIP은 임의로 초기화된 모델에서 마스크를 얻는다는 점입니다 (pre-selected mask).

Follow-ups of LTH and SNIP

LTH와 SNIP 이후에는 크게 두 가지 방향으로 연구가 진행되고 있습니다. 첫번째 방향은 LTH를 더 큰 dataset과 큰 model에 (e.g., ResNet50 on ImageNet) 대해서 적용하거나 NLP같은 non-vision domain에 적용하고, LTH의 이론적인 기반을 제안하는 방향입니다. 어떤 사람들은 LTH에 비판적인 입장을 갖고 유효성 검사를 하는 방향으로 연구를 진행합니다. 두번째 방향은 SNIP에서 사용되는 pruning criteria를 더 개선하는 쪽으로 연구가 진행되고 있습니다.

Dynamic masks

LTH와 SNIP에서 mask는 학습하는동안 고정되어 (static mask) 있습니다. 어떤 연구자들은 학습하는 동안 dynamic and adaptive mask를 선택하는 게 학습을 더 잘하게 만든다고 주장합니다. 그래서 static과 dynamic mask 두가지 모두 연구되고 있는데, 이 방법들을 합쳐서 Sparse Training이라고 부릅니다

Sparse Selection

연구자들이 LTH를 실험을 통해 이해하려고 시도하는 과정에서 신기한 사실이 하나 발견되었는데, LTH에서 wining ticket에 의해 선택된 sparse network는 추가적인 학습없이 좋은 성능을 낸다는 것이었습니다 (Strong LTH). 이 사실로 인해서 추가적인 학습 없이 sparse network를 이용하는 방향으로 연구가 진행되고 있는데, 이 방향을 Sparse Selection이라고 부릅니다.

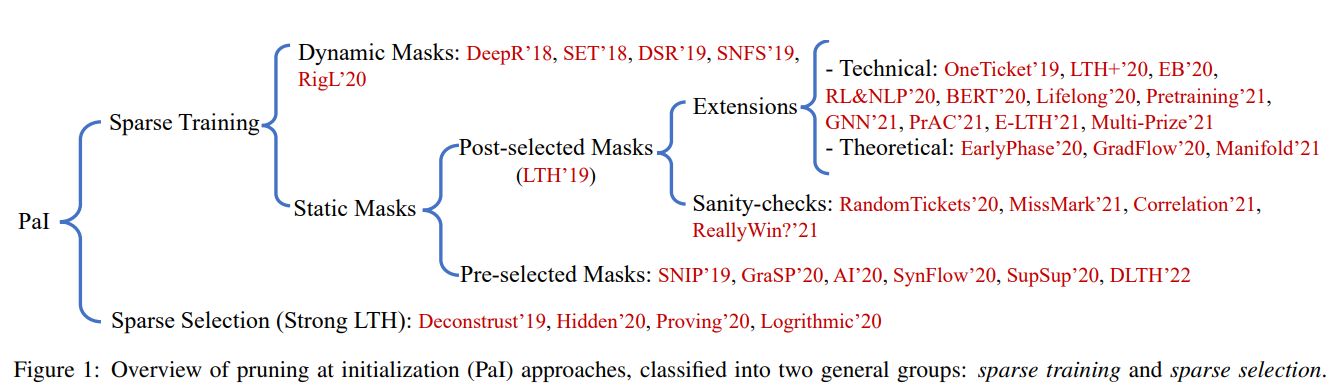
현재 PaI 연구 방향은 Sparse Training과 Sparse Selection으로 나누어집니다. 이걸 Tree 형태로 나타내면 다음 그림과 같습니다.

3.2. Sparse Training

3.2.1. Static masks: post-selected

Lottery Ticket Hypothesis (LTH)에서 주장하는 것은 다음과 같습니다.

임의로 초기화된 dense network는 sub-network (winning tickets)를 포함하는데, 해당 sub-network를 비슷한 iteration으로 혼자 학습했을 때 (trained in isolation) test data에 대해서 original network와 견줄만한 성능에 도달할 수 있다

LTH에서 Pruning은 3단계로 나누어집니다.

(1) 임의로 초기화된 네트워크를 수렴할 때 까지 학습한다.

(2) Magnitude pruning을 사용해서 mask를 얻는다.

(3) 네트워크를 다시 초기화하고 (2)에서 얻은 mask를 사용해서, 모델을 다시 학습한다.

(1), (2), (3) 과정이 iterative pruning 형태로 반복될 수도 있습니다.

LTH 영향을 받아서 Sparse Training이라는 연구분야가 생겼는데 이 분야는 두가지로 나뉩니다. 하나는 LTH의 정당성을 규명하거나 더 확장하는 방향이고, 다른 하나는 LTH에 대해 의심을 하면서 유효성 검사를 하는 방향입니다. 이거에 해당하는 것이 Figure 1 Tree 구조에서 Extensions과 Sanity-checks입니다.

Extensions

초기 LTH 방법은 MNIST 혹은 CIFAR-10 같은 작은 데이터셋에서 검증을 했습니다. 이후에 큰 데이터셋으로 확장해서 적용할 때, 초기 weight를 사용하지 않고 몇 epoch 하급한 후에 weight를 사용해서 ResNet50을 갖고 ImageNet에 적용했습니다. 또한 [Yu et al., 2020] 에서는 NLP와 RL에서도 lottery ticket 현상이 일어난다는 것을 발견해서, 성능을 유지한 채 transformer를 압축하는데 LTH를 사용했습니다. [Chen et al., 2021b]는 LTH를 사용해서 GNN에서 adjacency matrix와 모델 파라미터를 동시에 pruning하는 방법을 제시했습니다.

LTH의 pipeline인 train-prune-retrain 과정이 비용이 많이 들어서, [Zhang et al., 2021b]는 Pruning Aware Critical (PrAC) set을 도입했는데, 이 데이터셋은 학습 데이터의 35~80%정도의 양이고 이를 이용해서 학습 iteration을 60~90% 정도 단축시켰습니다. 게다가, PrAC set은 다른 네트워크에 대해서도 적용이 가능하다는 걸 발견했습니다. 유사하게 E-LTH [Chen at al., 2021c]에서는 다른 네트워크로 일반화가 가능한 winning ticket을 찾으려고 시도했습니다. 하나의 network에서 찾은 sparse 구조를 같은 family에 속하지만 depth나 width가 다른 네트워크에 적용해서 비슷한 성능을 내는데 성공했습니다. 또한 [You et al., 2020]는 학습 초기단계에서 비용이 적은 학습 전략으로 winning ticket을 빠르게 찾는 방법을 제시했습니다. 이 방법을 사용해서 4.7배정도 에너지를 절약하면서 비슷한 성능을 유지하는데 성공했습니다.

그 외에도 LTH를 이론적으로 이해하려는 시도들이 있었습니다. [Evci et al., 2020b]는 LTH가 왜 가능한지를 gradient flow를 통해 설명했고, [Zhang et al., 2021a]는 LTH의 정당성을 동역학계 이론 (dynamical systems theory)과 inertial manifold 이론을 통해 정당화 했습니다.

요약하면 LTH를 확장시키려는 시도들은 주로 LTH + X (LTH를 다른 task, 다른 학습 setting으로 확장), 더 적은 비용으로 ticket을 얻는 방법, LTH에 대한 심도깊은 이해로 이루어졌습니다.

Sanity-checks

LTH의 유효성은 실험 환경에 많이 영향을 받습니다. 이런 이유로 인해서 LTH에 관해서 논쟁이 많았습니다. [Gale et al., 2019]는 LTH 실험 결과를 재현할 수 없다고 보고했고, [Liu et al., 2021]는 학습률이 크지 않을 때 LTH에서 초기 weight와 마지막 weight 사이에 상관관계가 있다는 걸 발견했습니다. 이 결과를 기반으로 그들은 “winning ticket은 DNN pre-training이 충분하지 않았을 때만 존재한다. 잘 학습된 DNN에서는 winning ticket이 존재하지 않는다.”고 결론지었습니다. 앞선 연구의 영향을 받아서 [Ma et al., 2021]은 learning rate, training epoch, capacity, residual connection 같은 hyper parameter 값에 따라 winning ticket이 존재여부가 결정된다는 구체적인 증거를 제시하고, LTH를 적용할 때 하이퍼 파라미터 선택에 대한 가이드라인을 제시했습니다.

3.2.2. Static masks: Pre-selected

Static masks는 SNIP의 영향을 받아서 탄생했습니다. SNIP에서는 pruning criterion 기준을 connectivity sensitivity라고 부르는데, 이것이 의미하는 바는 특정 weight를 제거했을 때 loss 변화가 가장 적은 weight를 제거하자는 것입니다. 이 방법은 네트워크를 처음에 초기화한 이후에 각 weight 값을 pruning criterion에 따라 할당하고, 이후에 학습을 하면서 pruning ratio만큼 weight를 제거합니다. 이후에 [Wang et al., 2020]는 학습 초기에 loss 값보다는 training dynamics가 중요하다고 주장하면서 gradient signal preservation (GraSP)라는 방법을 제시합니다. 이 방법은 이전에 Hessian 기반으로 loss를 통해 제거할 weight을 판단하는 방법과는 다릅니다.

이와는 별개로 [Lee et al., 2020] 에서는 SNIP의 feasibility를 signal propagation을 통해 설명했습니다. 그들은 pruning을 적용하면 네트워크의 dynamical isometry를 손상시킨다는 증거를 찾아내서, 데이터와 독립적으로 초기화하는 방법인 approximated isometry (AI)를 제시했습니다. 이외에도 각 task별로 mask를 선택하는 방법 같은 것이 연구되었습니다.

정리하자면 PaT와 유사하게 Static mask에서는 pruning criterion를 어떻게 설정할 것 인지에 관한 연구가 진행되고 있습니다.

3.2.3. Dynamic masks

Sparse Training의 다른 유형으로는 학습 과정중에 mask를 변경할 수 있는 방향입니다. DeepR에서는 학습 도중에 stochasitc parameter를 통해 mask를 parameterization했고, SET에서는 magnitude pruning을 적용하면서 임의로 네트워크의 깊이를 조정하는 방식을 제시했습니다. DSR에서는 하이퍼 파라미터 없이 layer마다 sparsity 비율을 adaptive 방식으로 할당했습니다.

Dynamic masks의 본질적인 아이디어는 값이 0이된 파라미터가 다시 학습에 사용될 수 있다는 점입니다. 이 아이디어는 PaT에서도 있었다가, PaI에 적용되기 시작했습니다. 학습 과정중에 mask가 주기적으로 바뀌기 때문에 pruning criterion 비용이 크면 안됩니다. 그래서 모든 criteria는 학습 과정에서 쉽게 이용이 가능한 magnitude 혹은 gradient 기반으로 설계되었습니다.

3.3. Sparse Selection

Sparse Training은 dense model에서 sub-network를 선택한 후에 추가적인 fine-tuning 과정이 필요합니다. Sparse Selection에서는 파라미터를 최적화 하는 대신에, network topology를 최적화 하는 방향으로 연구가 진행되고 있습니다. 여기서 해결하려는 문제는 다음과 같습니다.

Dense 네트워크가 임의로 초기화되었을 때, 추가적으로 학습할 필요가 없는 sub-network를 찾자.

이런 연구 방향은 [Zhou et al., 2019] (Deconstruct)에서 LTH를 이해하려고 시도하다가, 추가적인 학습 없이 높은 accuracy를 확보한 sub-network를 우연히 발견한 이후로 시작되었습니다. 이것이 의미하는 바는 network 파라미터는 임의의 값이지만, 선택된 sub-network 구조는 임의로 선택된 것이 아니라는 것입니다. 다시말해서, sub-network를 찾는 과정이 학습의 일종이라는 의미입니다. 그래서 Zhou는 이를 supermasks라 부르고, mask를 최적화해서 supermasks를 찾는 알고리즘을 제시했습니다.

Zhou 방법은 MNIST 혹은 CIFAR 같은 작은 dataset에서 검증되었는데, 이후에 [Ramanujan et al., 2020] 에서는 random Wide ResNet50과 ImageNet에 적용을 했습니다. Ramanujan은 각 파라미터마다 trainable score를 도입해서 loss function을 최소화 하는 방향으로 score를 업데이트 했습니다. Trainable score는 네트워크 구조를 찾는데 사용이 됩니다. 이 방법을 ResNet50에 사용해서 ResNet34보다 작은 sub-network을 선택했는데, 해당 sub-network가 ImageNet을 기준으로 학습된 일반적인 ResNet34보다 top-1 accuracy 측면에서 나은 성능을 보였습니다. 이 연구 결과를 기반으로 논문에서는 LTH의 강력한 버전인 strong LTH를 제시합니다.

임의로 초기화된 over-parameterized network에는 좋은 성능을 가진 (competitive accuracy) sub-network가 존재한다.

위의 연구에 영향을 받아서 [Malach et al., 2020]는 strong LTH의 이론적인 근거를 제시하면서 “임의로 초기화된 네트워크를 pruning 하는 것이 학습을 통해 weight를 최적화 하는 것만큼 강력하다”고 주장했습니다.

4. Summary and Open Problems

4.1 Summary of Pruning at Initialization

Sparse Training: Much overlap between PaI and PaT.

PaT의 주요한 목적은 효율적인 inference 이지만, PaI의 주요한 목적은 효율적인 학습입니다. 이런 차이가 있음에도 불구하고, PaI에서 사용되는 방법은 PaT의 영향을 많이 받았습니다. 2.1에서 다룬 pruning의 4가지 중요한 측면에서, pruning ratio, criterion, schedule 부분은 PaI와 PaT 거의 차이가 없습니다. 하지만 sparsity structure 측면에서는 차이가 있습니다.

Structured Pruning은 PaI에서 관심대상이 아닙니다. 왜냐하면 layer마다 sparsity ratio를 주어서 PaI를 적용하는 것은 dense network를 처음부터 학습하는 것으로 귀결되기 때문입니다. 그래서 PaI 연구는 대부분 unstructured pruning 기반으로 진행이 되고있고, 잘알려진 LTH 또한 unstructured pruning에 대해서만 적용이 됩니다. Filter 기반 pruning에 적용되는 이론의 정당성을 증명한 연구는 알려지지 않았는데, 그 이유는 명확하지 않습니다.

Sparse Selection: Significant advance of PaI vs. PaT.

PaT를 적용할 때 밑바탕이 되는 믿음은 초기 모델에서 학습한 지식을 남아있는 파라미터가 보유하고 있다는 것입니다. 지식을 상속하는 것이 처음부터 학습하는 것보다 좋다고 많은 연구결과가 증명하고 있기 때문에 이런 믿음이 있습니다.

이와는 대조적으로 PaI에서는 초기 단계의 파라미터를 이용해서 지식을 상속합니다. 그러면 초기 단계에 있는 파라미터는 충분한 지식을 보유하고 있다는 것일까요? 더 근본적으로는 뉴럴네트워크가 무에서 지식을 학습하는 것인지, 아니면 모델이 원래 소유하고 있던 지식을 드러내는 것인지에 관해서도 질문을 할 수 있습니다. PaT는 전자를 암시하고, PaI는 후자를 암시합니다. 저자는 이런 질문들에 대한 답을 통해 deep neural network에 대해서 좀 더 이론적인 이해로 인도할 수 있다고 믿고있습니다.

4.2. Open Problems

Same problems as pruning after training

PaI와 PaT가 겹치는 부분이 많기 때문에, PaT에서 있는 open problem들이 PaI에도 똑같이 적용이 됩니다. 2.1에서 말한 4가지 주제에 관해서 계속 연구되고 있습니다.

Under-performance of PaI

PaI의 아이디어는 실용적인 관점에서 매력적이지만, 여전히 PaT보다 성능이 좋지 않습니다. 예를들어 [Wang et al., 2020] 에 따르면 SNIP과 GraSP는 Cifar-10/100에 대해서 VGG19와 ResNet32에 적용했을 때 전통적인 pruning 방법인 OBD와 MLPrune보다 성능이 꾸준하게 좋지 않다 (해당 방법이 심지어 SOTA도 아닙니다)는 연구결과가 있습니다.

Under-development of sparse libraries

Sparse training의 잠재적인 가능성에도 불구하고, 실용적으로 구현하지 못했습니다. SNFS에서는 5.61배 빠르게 학습을 할 수 있다고 주장했지만, sparse matrix multiplication이 개발이 많이 되지않아서, 빠르게 학습하는 이점을 실제로 적용하지 못하고 있습니다. 이 논문 저자들 지식을 기준으로, sparse training을 사용해서 실제로 학습 시간을 단축시켰다는 (wall-time speedup) 연구결과가 거의 없다고 합니다. 그래서 sparse training library를 개발하는 것이 중요하다고 볼 수 있습니다.

5. Conclusion

이 논문에서는 PaI 기법에 대해서 정리했습니다. PaI 기법에 대해서 Sparse Training과 Sparse Selection으로 나누어서 정리를 했고, PaT와 비교를 통해 어떤점이 다른지 설명했습니다.