1. Introduction
현대의 딥러닝 모델은 대부분 크기가 커서 메모리를 많이 차지하고 학습과 추론 단계에서 계산량이 많이 필요합니다. 이런 이유 때문에 모델을 경량화 하려는 연구들이 많이 진행 되었고, 그 중 한가지 연구방향이 Sparsification 입니다. Sparsification은 고차원 feature space에서 몇개의 파라미터 값을 0으로 만들어서 전체가 아니라 일부만 가지고 학습과 추론을 하는 방법입니다. 이 방법을 통해 모델의 complexity를 낮출 수 있습니다. 본 논문에서는 Sparsification을 통해 모델을 경량화하는 여러가지 방법에 대해 정리했습니다.
2. Overview of Sparsity in Deep Learning
Sparsification을 통해 얻을 수 있는 점은 (1) generalization and robustness 향상 (2) 학습과 inference performance 향상 두 가지가 있습니다.
2.1. Generalization
일반화 성능은 딥러닝 모델의 가장 중요한 측면 중 하나입니다. 일반화 성능은 학습 때 사용하지 않았던 데이터에 대해서 모델의 성능을 통해 측정이 됩니다.

Sparsification을 적용하면 초기에는 sparsification이 학습 노이즈 제거역할을 해서 accuracy가 증가합니다. 모델의 크기를 작게하는 것이 regularizer 역할을 해서 모델이 좀 더 데이터의 일반적인 측면을 학습할 수 있도록 도와주는 역할을 합니다 (위의 그림에서 A 영역에 해당). 점점 더 증가시키면 모델의 performance는 안정화되지만 accuracy가 살짝 감소하는 B영역에 도달하고, 여기서 sparsity를 더 증가시키면 accuracy가 갑자기 많이 감소합니다 (C영역).
계산량 관점에서 살펴봤을 때도, 위의 그림과 비슷한 커브가 그려질 것입니다. 초기에 sparsity가 적을 경우에는 sparse structure를 저장하고 sparse computation을 하는데 필요한 오버헤드가 있기 때문에 계산량은 천천히 감소할 것입니다. Sparsity를 중간 정도로 증가시키면 계산량을 많이 감소시킬 수 있고, 최대로 증가시키면 storage와 sparse computation 오버헤드로 인해서 계산량의 변화가 거의 없을 것입니다.
2.2 Performance and model storage
Sparsification을 통해 뉴런을 제거할 때, 어떤 구조적인 방법으로 뉴런 전체를 없애거나 필터를 제거하면, sparse structure를 dense structure로 변환할 수 있습니다. 하지만 구조는 신경쓰지 않고 임의로 제거한다면 남아있는 뉴런의 index를 저장해야 해서 추가적인 storage overhead가 필요합니다.
크기가 n인 공간에 m개의 non-zero element를 저장하는 방법은 n개의 bitmap을 사용하는 방법부터 \(mlog(n)\) bit를 사용한 absolute coordinate scheme까지 다양한 방법이 있습니다. 그리고 최적의 저장 방법은 sparsity 정도에 따라 달라집니다.

만약에 n개의 element를 저장할 수 있는 공간에, 각 element가 k bit인 m개의 element를 저장하는 상황을 가정해보겠습니다. 어떤 전략을 사용할지는 하드웨어적인 요소와 저장해야할 파라미터의 크기에 따라 다르지만, 그림 5에서 대략적으로 sparsity의 강도에 따라 최적의 전략을 표시했습니다.
가장 단순한 전략은 element 마다 bit 하나를 사용해서 각 element의 존재여부를 표시하는 bitmap (BM) 방법입니다. BM은 상대적으로 dense한 뉴런을 저장할 때 적합하고 추가적으로 \(n\) bit가 필요합니다.
그 다음으로 단순한 전략은 0이 아닌 element를 absolute offset과 함께 저장하는 방법인 coordinate offset (COO) 입니다. 이 전략은 sparsity가 엄청 높을 때 가장 효율적인데, 왜냐하면 \(m\left\lceil\log _2 n\right\rceil\)만큼 추가적인 bit가 필요하기 떄문입니다.이 전략은 runlength encoding (혹은 delta coding으로도 알려졌습니다)으로 확장될 수 있는데, 이 방법은 두 원소의 차이만큼 저장이 됩니다. 만약에 index를 기준으로 원소들을 정렬하고 이웃하는 두 원소의 인덱스 차이의 최대값이 \(\hat{d}\) 라면, \(m\left\lceil\log _2 \hat{d}\right\rceil\) bits를 사용해서 sparse matrix를 나타낼 수 있습니다.
만약 offset이 변화하는 정도가 매우 크다면, zero-padded delta offset을 사용해서 사용하는 bit 수를 \(\left\lceil\log _2 \bar{d}\right\rceil\)으로 줄일 수 있습니다. 여기서 \(\bar{d}\) 는 평균적인 차이를 나타내고, \(\bar{d}\) 보다 멀리 떨어졌을 경우에 0의 값을 추가합니다. 이 방법의 오버헤드는 distance 분포에 따라 달라지고, 패딩이 적게 필요한 경우에 이 전략이 효율적입니다.
Sparsity가 높은 행렬에 대해서는 **compressed sparse row (CSR), compressed sparse column (CSC),** 혹은 fiber 기반의 전략들은 행렬과 tensor의 인덱스를 저장합니다. 이런 방법들을 dimension-aware scheme이라고 부르는데, CSR을 예로 들어서 설명을 해보겠습니다. CSR은 \(n_c \times n_r\) 행렬을 column과 row 배열을 사용해서 나타냅니다. Column 배열은 길이가 m이고 \(\left\lceil\log _2 n_c\right\rceil\) bits안에 각 값의 column index를 저장하고, row 배열은 길이가 \(n_r\)이고 \(\left\lceil\log _2 m\right\rceil\) bits안에 각 row의 offset을 저장합니다.
만약에 \(n=10^8, k = 8\)인 상황을 가정해보면 dense representation의 경우 bitmap의 storage overhead가 가장 작을 것입니다. Bitmap은 10~70% 정도의 sparsity에서 효율적이고, delta encoding scheme은 80%보다 큰 sparsity에서 효과적입니다. Offset index 전략이나 dimension-aware 전략은 그 보다 큰 sparsity에서 효율적인데, 실제로 그 정도의 sparsity를 가진 deep learning model이 존재할지는 모르겠습니다.
2.3. What can be sparsified?
이번 문단에서는 Deep learning 모델에서 어떤 요소에 sparsification을 적용할 수 있는지 정리해보겠습니다. 먼저 여기서는 Model sparsification과 ephemeral sparsification을 구분하겠습니다.
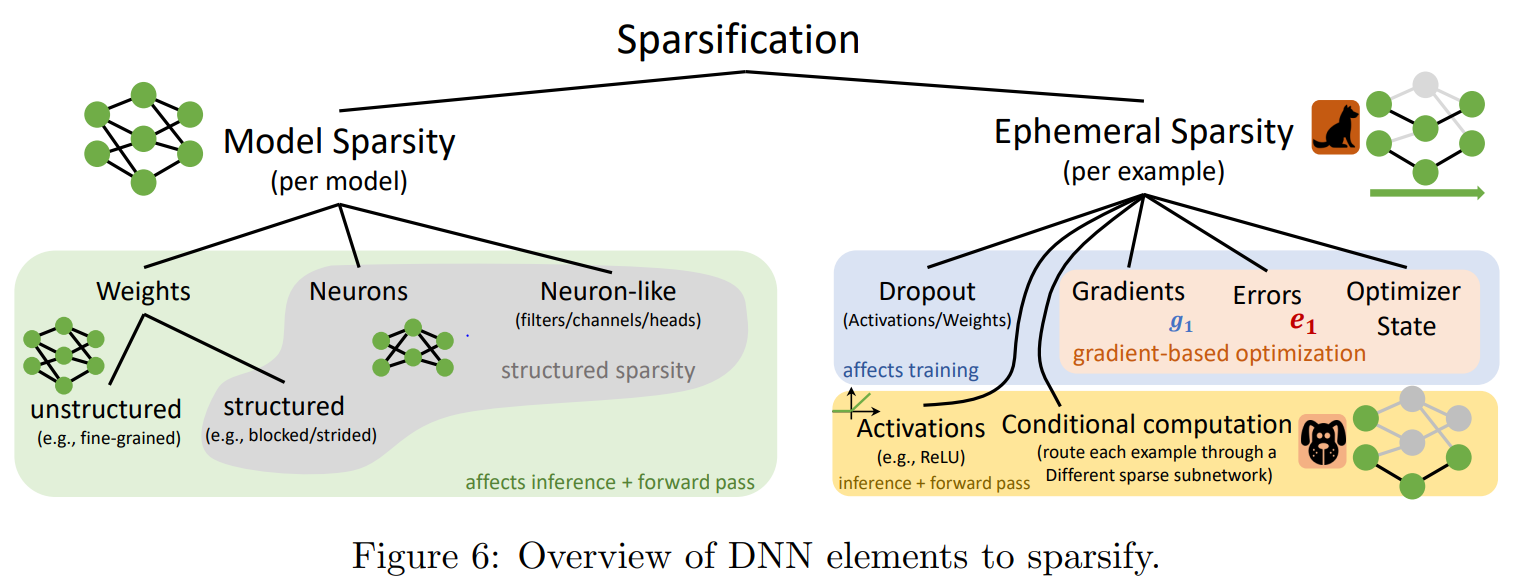
Model sparsification은 모델을 변경하는 거고 NAS의 일종으로 여겨집니다. 여기서는 파라미터와 뉴런을 sparse하게 만듭니다. Weight sparsification에도 두 가지 종류가 있는데, 임의의 weight을 sparsify하면 모델의 구조가 사라지게 돼서 남아있는 weight마다 index를 저장해야 합니다. 이러면 index를 저장하는데 저장비용이 들고, dense computation에 최적화된 하드웨어에서는 연산속도가 느릴 가능성이 있습니다. 그래서 structured sparsification을 통해 index storage overhead를 줄이고 연산을 빠르게 수행하는 방법이 많이 연구되었습니다. 이런 방법들은 챕터 3, 4에서 자세히 살펴보겠습니다.
Ephemeral sparsification은 어떤 하나의 example을 계산하는 도중에 sparsification을 수행하는 방법입니다. 예를들어 ReLU 혹은 rounding SoftMax는 특정 threshold에 대해서 0을 할당하기 때문에 sparsification 방법입니다. 또 다른 ephemeral sparsification 방법은 gradient 기반 학습과 관련이 있습니다. Back-propagation 과정에서 weight을 업데이트 할 때 부분적으로 바꿔주거나, 그레디언트 값이 커질 때까지 파라미터 update를 지연시키는 방법이 있습니다 (5.3 챕터). 이 방법은 forward 할 때 ephemeral sparsification을 적용하는 것과 비슷한 영향을 주고, 특히 분산 환경에서 많은 성능 향상을 가져왔습니다. 또 다른 방법으로는 conditional computation 방법이 있는데, 이 방법은 모델이 example마다 sparse 계산 경로를 동적으로 결정하는 방법입니다. 이런 방법들에 대해서는 챕터 5에서 살펴보겠습니다.
2.4. When to sparsify?
Ephemeral sparsity는 example마다 동적으로 파라미터를 업데이트하지만, model sparsity는 주로 NAS 같은 절차를 수행합니다. 주로 pruning schedule을 통해 model sparsity가 이루어지는데, 3가지 종류로 나눌 수 있습니다.
2.4.1. Sparsity After Training
Train-then-sparsify는 모델을 \(T\) iterations 만큼 학습한 후에 sparsification을 적용하고 fine-tuning을 통해 모델의 성능(accuracy)을 향상시키는 과정입니다. 이런 방법들은 inference 하는 동안 모델의 accuracy와 generalization 성능을 향상시키는데 목적을 두고 있습니다.
2.4.2 Sparsify During Training
Sparsify-during-training (Sparsification schedule)방법은 학습을 시작하고 모델이 수렴하기 전에 sparsification을 적용하는 방법입니다. 일반적으로 Train-then-sparsify 방법보다 연산량이 적지만, convergence 했을 때 성능이 안 좋은 경우가 있고 하이퍼파라미터에 민감하다고 알려져있습니다. 게다가 dense model 전체를 메모리에 계속 유지해야 하기 때문에, capacity가 작은 장치에서는 사용할 수 없습니다. 어떤 방법들은 weight 혹은 gradient를 pruning 하는 대신에, 학습 가능한 binary mask를 사용해서 pruning을 수행합니다.
Sparsification schedule에서 중요한 것은 얼마나 빠르게 많은 뉴런을 제거할 것인지 입니다. Prechelet (1997)은 전체 학습 과정동안 고정된 pruning schedule을 사용하면 모델의 generalization 성능이 많이 떨어질 수 있다는 걸 실험에서 관측했습니다. 그래서 generalization loss를 사용해서 pruning rate를 조절했는데, generalization loss가 커지면 pruning rate를 증가시키는 방식을 사용했습니다. 이 방법을 사용해서 모델의 generalization 성능을 많이 향상시켰습니다.
다른 방법으로는 Iterative hard thresholding (IHT) 방법이 있는데, 이 방법은 dense와 sparse 방법이 다음과 같이 반복적으로 적용됩니다.
(1) Magnitude를 기준으로 top-k weight을 제거하고, 제거한 sparse network를 s번 만큼 fine-tuning 합니다.
(2) Pruned weight를 다시 복원시켜서 dense network를 만들고 d번 만큼 학습합니다.
(1), (2)번 과정을 \(i\)번동안 반복하는데, (1)번 과정은 네트워크에 regularization을 적용하는 과정이고, (2)번은 더 좋은 representation을 학습하기 위한 방법입니다. 이외에도 dense-sparse-dense 순서로 학습하는 방법을 제시한 연구도 있는데, 이런 방법들은 일반적인 SGD 알고리즘에서 모델의 학습능력 (learnability)을 증가시키는 걸 목표로 하고있습니다.
뇌가 나이가 들면서 신경가소성이 감소하는 것처럼, 딥러닝 모델도 학습 초기에 중요한 파라미터나 구조가 결정된다고 주장하는 논문들이 있습니다. 특히 Shwartz-Ziv and Tishby (2017) 에서는 SGD기반 학습 방법이 2페이즈로 나누어진다고 주장합니다.
(1) 학습 error를 빠르게 최소화하는 drift phase
(2) 내부 representation을 압축하는 diffusion phase
이런 이론들은 학회에서 논쟁의 여지가 남아있지만, 많은 실험적인 증거들이 발견되고 있습니다. 예를들어 Michel (2019) 에서는 트랜스포머의 중요한 head가 첫 10 epoch 안에 결정된다는 걸 보여줬고, Ding (2019b) 에서는 학습 과정에서 나중에 제거될 뉴런들이 초기에 발견되었고 이후에 추가된 뉴런이 거의 없다는 것을 실험에서 발견했습니다. 이 논문에서는 이런 현상을 early structure adaptation이라고 부릅니다.
You (2020)은 early structure adaption을 이용해서 pruning을 수행했는데, 그 방법은 실제 학습을 진행하기전에 논문에서 제시한 low-cost approximation training 방법을 통해 sparse structure를 발견하고 그 구조를 기준으로 네트워크를 학습합니다. 그리고 이후에 Li (2020)은 초기에 learning rate를 크게 주면 모델이 초기에 sparse structure를 쉽게 학습을 하게 되는데, 이후에 learning rate를 낮춰주면서 모델을 학습했습니다.
2.4.3. Sparse Training
Fully-sparse training 방법은 sparse model로 시작해서 학습 과정동안 element를 제거하거나 추가하는 방법입니다. 이런 방법들은 하이퍼 파라미터, 스케쥴링, 초기화 방법을 잘 설정해줘야 하지만, sparse model 형태로 학습을 시작한다는 장점이 있습니다. 여기 논문에서는 static sparsity와 dynamic sparsity를 구분하겠습니다. Static sparsity는 학습 시작전에 pruning을 통해 모델 구조를 고정시키고 학습 과정동안 모델 구조를 변화시키지 않고, dynamic sparsity는 다양한 기준에 따라 학습하는 동안 element를 제거하거나 추가하면서 모델 구조를 변화시킵니다. 자세한건 챕터3과 4에서 살펴보고, 여기서는 static sparsity에 대해서만 살펴보겠습니다.
Static sparsity 방법은 네트워크의 학습이 시작되기전에 sparse structure를 결정하는 방법입니다. Liu (2019)은 over-parameterized model을 학습한 후에 pruning을 적용하는 과정이 꼭 필요한지 의문이 들었고, 처음부터 작은 네트워크를 학습하면 어떤지 생각해봤습니다. 그래서 몇가지 실험을 통해 sparse model을 처음부터 학습하면 추가적으로 pruning을 적용하지 않아도 CIFAR-10과 ImageNet에 대해서 성능이 어느정도 확보된다는 것을 보여줬습니다.
SNIP에서는 학습전에 데이터를 기반으로 네트워크의 unstructured sparse structure를 찾는 방법을 제시했습니다. 어떤 파라미터가 loss에 끼치는 영향이 작으면 해당 파라미터를 제거하는 방식인데, 측정하는 방식은 single batch에 대해 대한 \(w\)의 중요도를 \(I_w^{(1)}=\left|\frac{\partial L}{\partial w} w\right|\) 을 이용해서 계산합니다 (30년전에 Mozer and Smolen-sky가 제시한 방법). 이를통해 중요도가 낮은 파라미터를 제거하고 학습을 시작하는 방식입니다.
Wang (2020) 은 sparsity가 매우 큰 상황에서 SNIP 방법이 특정 layer의 거의 모든 뉴런을 제거해서 gradient가 네트워크 전체로 퍼지는 것 (gradient flow)을 방해한다고 주장했습니다. 그래서 sparsity가 높은 상황에서는 임의로 pruning을 하는 것보다 SNIP의 성능이 좋지 않다는 걸 발견했습니다. 이를 해결하기 위해 제시한 방법은 gradient 흐름을 막는 bottleneck (layer의 뉴런이 거의 모든 0인 영역)을 미리 파악해서 해당 bottleneck layer에 있는 뉴런은 제거하지 않는 방법입니다.
2.4.4. General Sparse Deep Learning Schedules
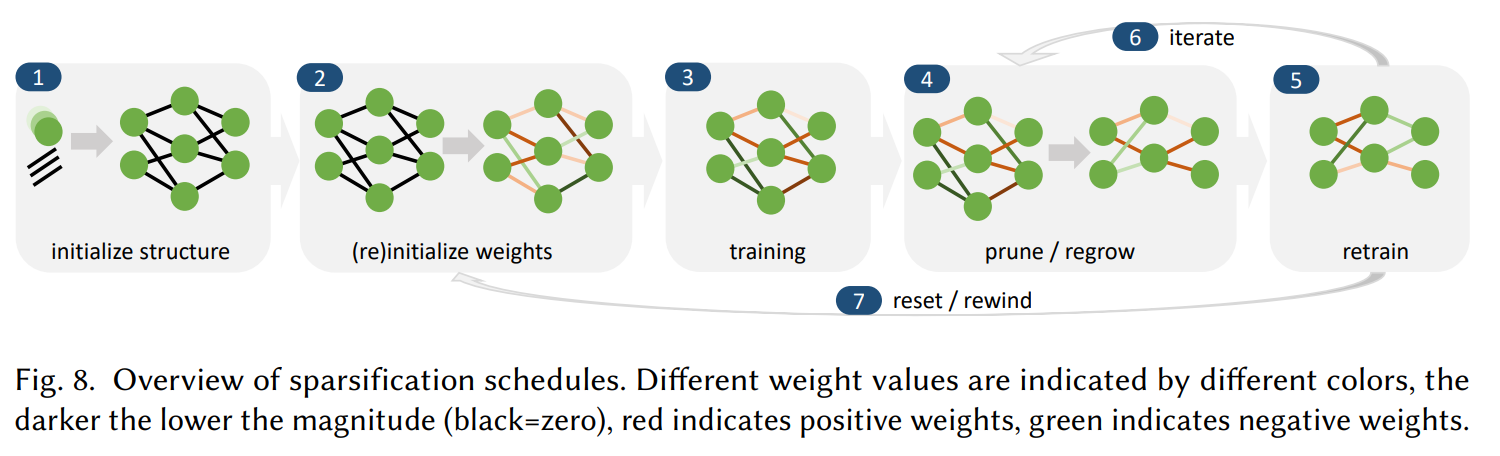
위의 그림은 pruned network를 학습하는 전반적인 과정을 나타냅니다. 각 step은 생략될 수도 있고 여러번 반복될 수 있습니다. (1)번의 경우에 네트워크 구조를 기술한 정보를 디스크에서 가져오거나 SNIP 같은 방법을 통해 sparse network를 생성할 수 있습니다. (2)번은 파라미터를 임의로 초기화 하거나 pre-trained weight을 사용할 수 있습니다.
(3)번은 네트워크가 수렴할 때 까지 학습을 반복하는 것인데, 일반적인 dense network를 학습알고리즘을 사용하거나, regularization 처럼 sparsity를 유도하는 알고리즘도 사용이 가능합니다. (4)는 네트워크 안에 구성요소들을 pruning하거나 regrow하는 단계입니다. 챕터 3, 4에서 자세히 설명할 예정입니다.
(5)번은 수렴할 때 까지 네트워크 구조를 고정시키는 과정입니다. 일반적으로 생략되는 단계이지만 모델 정확도를 많이 향상시켜준다고 합니다. (6)번과 (7)번은 학습 과정을 반복하는 것입니다.
지금까지 소개한 방법들은 (4)번 단계에서 sparsification을 얼마나 주기적으로 적용할 것인지에 관한 횟수를 설정해줘야 합니다. Jin (2016)에서는 적절히 frequency를 바꿔가면서 pruning을 적용하는 것이 모델 퍼포먼스에 큰 영향을 미친다고 주장했습니다. 하지만 pruning 과정에서 사용되는 hyperparameter (frequency, mini-batch size 등)을 어떻게 최적의 값으로 설정할지에 관한 연구는 많이 진행되지 않았습니다.
3. Selecting Candidates for Removal
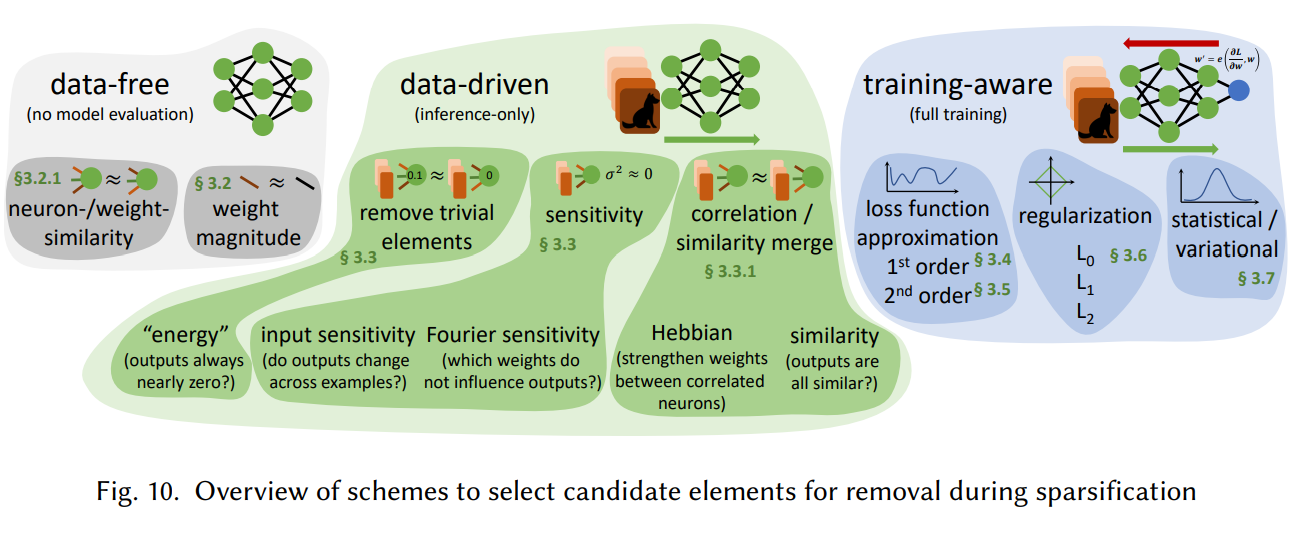
Gale (2019)에서 여러 sparsification 방법을 비교했는데 확실하게 누가 제일 좋다라고 말하기 어렵다고 결론을 지었습니다. 왜냐하면 네트워크 구조, 하이퍼 파라미터, learning rate schedule, task에 따라 성능이 전부 다르기 때문입니다. 그래서 여기서는 어느 방법이 제일 좋은지에 대해 설명하기 보다는, 각 방법의 아이디어와 특정 실험 환경에서 해당 방법이 어떤 성능을 냈는지에 대해 정리했습니다. 다음 그림은 제거할 뉴런을 선택할 때 사용하는 방법들의 개괄적인 요약입니다.
3.1. Structured vs Unstructured element removal
Section 2.2에서 봤던 것 처럼, unstructured sparse weight에서 0이 아닌 원소를 저장하려면 offset이 필요하고, unstructured weight을 연산에 사용하기 위해서 원래 structure를 고려하는 추가적인 processing 과정이 필요합니다. Structured sparsity는 structure를 고려해서 원소를 저장할 수 있기 때문에, 추가적인 offset이 많이 필요하지 않습니다. 하지만 structured removal은 특정 구조 형태로만 제거가 가능하기 때문에 degree of freedom이 낮아서 모델의 성능이 안좋을 가능성이 있습니다.
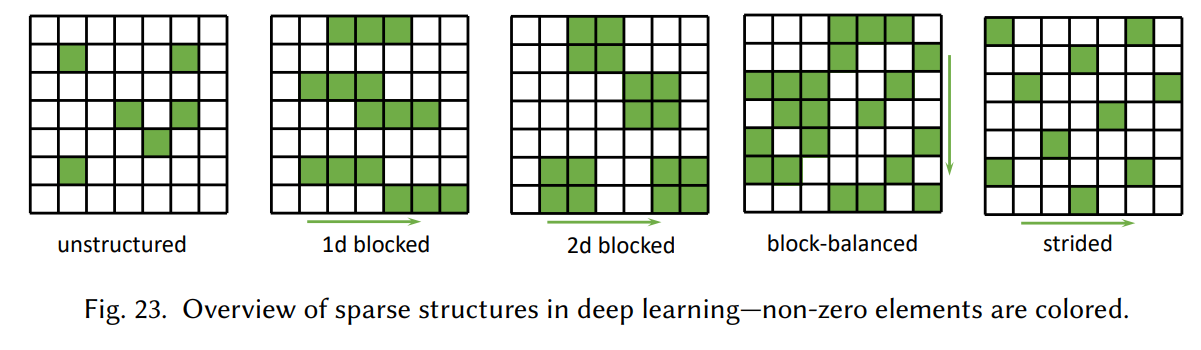
위의 그림은 unstructured 혹은 특정 구조 형태로 제거할 뉴런을 선택하는 방법들입니다. Block 구조의 경우에는 각 block마다 offset을 한번만 저장하면 되므로 블락의 크기가 B라면 unstructured sparsity와 비교해서 저장공간은 B만큼 줄어들게 됩니다. Strided 구조의 경우에는 첫번째 offset과 stride의 크기, 파라미터 값만 저장하면 weight 전체를 저장할 수 있어서 저장공간이 엄청나게 줄어들게 됩니다. Stride 구조를 사용하는 경우는 주로 channel 단위 sparsification, 연속하는 layer에있는 두 개의 feature 의 연결을 제거, 혹은 특정 stride마다 연속하는 layer의 두 feature 사이에 연결을 제거하는 경우입니다.
3.2. Data-free selection based on magnitude
Section 3.1에서 제시한 두 방법은 저장하는 방식과 제거하는 방식에 차이가 있지만, 근본적으로 제거할 뉴런을 선택할 때 고려하는 기준은 유사합니다. 가장 단순하고 효과적인 방법중에 하나는 absolute magnitude가 가장 작은 weight를 제거하는 것입니다. 이 방법은 단일 뉴런에 대해서도 적용이 가능하고, block이나 group 안에 있는 뉴런의 absolute magnitude를 합하는 형태로도 사용이 가능합니다.
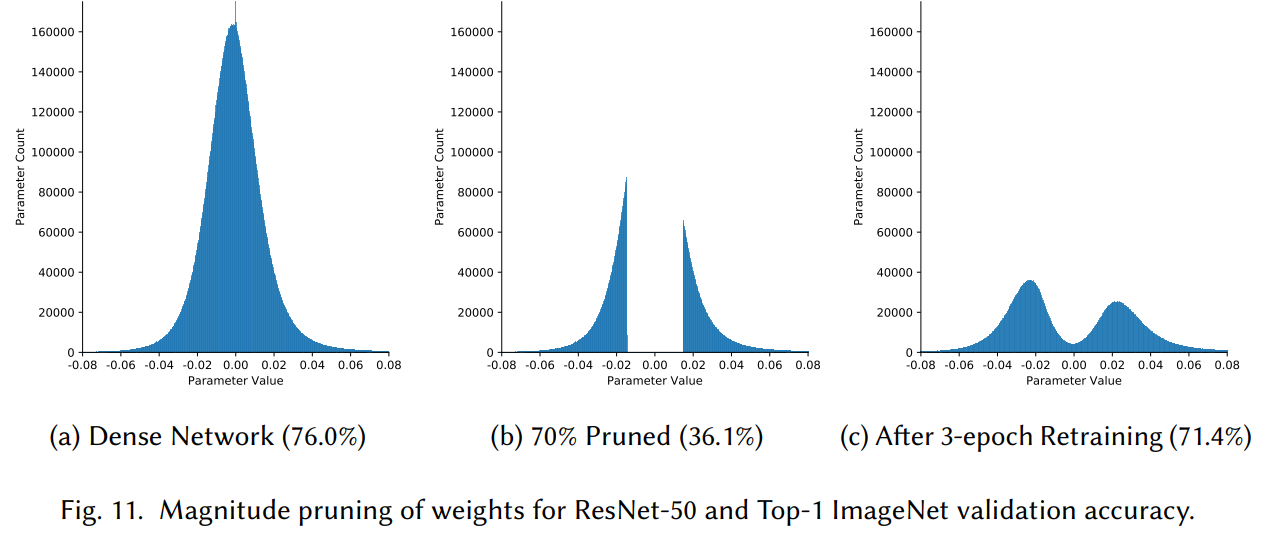
Weight 값의 분포는 보통 정규분포를 따르기 때문에, magnitude를 기준으로 pruning을 하면 값이 0 근처인 weight를 제거하게 됩니다. 위의 그림에서 (a)는 pruning 이전에 weight 값이 분포, (b)는 \(|w| \le x\)를 기준으로 pruning 이후에 분포, (c)는 retraining 이후에 분포를 나타냅니다. 여기서 중요한 것은 \(x\)를 어떻게 선택하는지에 관한 것인데, threshold를 \(w\)를 통해 parameterization해서 학습 과정동안 layer마다 학습하는 방법이 있고, reinforcement learner를 사용해서 각 layer마다 적합한 threshold를 찾는 방법이 있습니다.
Magnitude pruning 말고도 data 없이 pruning을 수행하는 방법들이 있습니다. Fully connected layer에서 N개의 output이 있는 layer에서 뉴런을 제거하고 싶을 때, N개의 output 뉴런의 input weight의 유사도를 계산해서 N x N 행렬 \(S\)를 만듭니다. 예를들어 \(S_{i,j}\)는 \(i\)번째 output을 생성하기 위해 사용한 weight와 \(j\)번째 output을 생성하기 위해 사용한 weight 사이에 유사도를 의미합니다. 이렇게 계산을 하고 유사도가 높은 뉴런 그룹을 만들어서, 그룹안에 대표 1개만 남겨두고 나머지 뉴런은 제거하는 방법입니다. 이 방법은 Srinivas and Babu가 2015년에 제시헀는데, 실험결과를 통해 유사한 뉴런은 불필요하다는 걸 주장합니다. 하지만 이 방법은 크기가 작은 네트워크에 대해서만 잘 적용이 되고, 크기가 커지면 적용이 안되는 현상이 있습니다.
Data-free 방법들은 효과적이고 SOTA 결과를 낼 때가 있지만, sparsity가 큰 경우에 좀 더 정확한 방법이 필요하고 pruning 이후에 re-training 과정에서 종종 비용이 많이 발생합니다.
3.3. Data-driven selection based on input or output sensitivity, activity, and correlation
Data를 고려한 selection 방법은 학습 데이터에 대해서 뉴런 output의 sensitivity 혹은 전체 네트워크의 sensitivity를 고려합니다. 뉴런의 값이 0에 가까우면 학습 데이터가 변해도 전체 네트워크 output에는 많이 영향을 끼치지 않기 때문에 sensitivity가 낮을 것입니다. 이런 이유로 인해서 sensitivity를 측정해서 제거할 뉴런을 선택합니다.
가장 단순한 방법으로는 전체 입력 데이터에 대해서 output에 변화가 거의 없는 뉴런의 경우, 해당 뉴런을 제거하고 일정한 상수값을 가진 bias로 대체하는 방법입니다. 이 방법을 좀 더 확장해서, 각 layer의 input이 변할 때 output이 거의 변하지 않는 뉴런을 삭제하는 방법도 있습니다. Han and Qiao (2013)는 FFT를 이용해서 입력 변화에 대한 출력 변화도를 측정했습니다.
다른 방법으로는 항상 같이 활성화되는 output을 제거하는 방법이 있습니다. 전체 학습 데이터에 대해서 대부분 output이 유사하면, 대표 뉴런 1개만 남겨두고 나머지 뉴런을 제거하는 방식으로 pruning이 수행됩니다.
마지막으로 연결된 뉴런 사이의 connection 강도를 측정해서, 약하게 연결된 뉴런의 weight는 제거하고 강하게 연결된 뉴런의 weight를 유지하는 방법이 있습니다.
3.4. Selection based on 1st order Taylor expansion
뉴럴네트워크를 학습할 때 gradient를 기반으로 학습하기 때문에 gradient를 통해 제거할 뉴런을 선택하면 계산비용을 줄일 수 있습니다. 보통 특정 weight 값이 변했을 때 loss값이 많이 변하지 않으면, 해당 뉴런이 중요하지 않다고 판단해서 제거를 합니다. 이때 weight에 대한 loss \(L(\mathbf{w})\)의 변화를 계산할 때 다음과 같이 근사할 수 있습니다.
\[\delta L=L(\mathbf{w}+\delta \mathbf{w})-L(\mathbf{w}) \approx \nabla_{\mathbf{w}} L \delta \mathbf{w}+\frac{1}{2} \delta \mathbf{w}^{\top} \mathbf{H} \delta \mathbf{w}\]여기서 \(\nabla_{\mathbf{w}} L\) 는 gradient, \(\mathbf{H}\)는 Hessian matrix입니다. Gradient만 사용해서 근사할 수도 있고, Hessian matrix까지 사용해서 더 정확하게 계산할 수도 있습니다.
변화를 계산할 때 가장 단순한 방법으로는 전체 학습 데이터에 대해서 gradient를 모두 더해서 변화가 적은 weight를 제거하는 방법입니다. 제거할 때는 각 weight마다 binary gating function을 사용합니다. 만약에 \(\alpha_i\)가 \(i\)번째 뉴런의 gate라고 하면 forward하는 방식을 \(f_l=\sigma_R\left(W_l \cdot \alpha \odot f_{l-1}\right)\) 으로 나타낼 수 있습니다. 이전 layer의 activation \(f_{l-1}\) 차원만큼 gate vector \(\alpha\)를 생성해서, 이전 layer의 output 중 어느 것을 현재 layer에 반영할지 선택을 한다는 의미입니다. Loss \(L\)에 대한 gate의 변화 \(\frac{\partial L}{\partial \alpha_i}\)가 크다면 해당 뉴런은 중요하고 작으면 제거해도 영향이 없다는 가정하에 pruning을 진행합니다.
Xu and Ho (2006)은 Jacobian matrix를 이용해서 제거할 뉴런을 선택하는 방법을 제시했습니다. Jacobian은 보통 full rank가 아니기 때문에 어떤 weight의 gradient는 서로 연관되어 있습니다. Jacobian matrix를 QR 분해를 해서 연관성이 있는 gradient를 제거하는 방법입니다.
3.5. Selection based on 2nd order Taylor expansion
Le Cun (1990)은 완전히 학습된 모델이 주어졌을 때, 중요하지 않은 weight를 선택하는 문제를 최적화 관점에서 접근했습니다.
\[\delta L=L(\mathbf{w}+\delta \mathbf{w})-L(\mathbf{w}) \approx \nabla_{\mathbf{w}} L \delta \mathbf{w}+\frac{1}{2} \delta \mathbf{w}^{\top} \mathbf{H} \delta \mathbf{w}\]위의 식에서 perturbation \(\delta \mathbf{w}\)는 \(i\)번쨰 뉴런을 0으로 만드는 방향으로 변한다고 가정하면 \(\delta \mathbf{w}=\left(0, \ldots,-\mathbf{w}_i, \ldots, 0\right)\)로 나타낼 수 있습니다. 완전히 학습된 모델이라는 가정이 있기 때문에, model이 local minimum에 있어서 gradient \(\nabla_wL=0\) 입니다. 그러므로 perturbation에 대한 loss의 변화는 다음과 같이 Hessian matrix를 사용해서 나타낼 수 있습니다.
\[\frac{1}{2} \delta \mathbf{w}_i^{\top} \mathbf{H} \delta \mathbf{w}_i\]이 값을 최소화하는 \(\mathbf{w}_i\)를 찾는 최적화 문제를 Lagrange multiplier를 사용해서 풀면 다음과 같은 saliency measure를 얻을 수 있습니다.
\[\rho_i=\frac{\mathbf{w}i^2}{2\left[\mathbf{H}^{-1}\right]{i i}}\]여기서 \(\left[\mathbf{H}^{-1}\right]_{i i}\)는 inverse Hessian matrix의 \(i\)번째 diagonal element입니다. 이 값을 내림차순으로 정렬해서 가장 낮은 weight를 제거하는 방법인데, 이 방법을 Optimal Brain Damage (OBD)라고 합니다.
위에 식에서 Hessian matrix가 identity인 경우에, weight의 magnitude가 가장 작은 weight를 제거하는 형태로 바뀌게 됩니다. 그래서 Magnitude pruning은 OBD의 특별한 경우라고 해석할 수 있습니다.
3.5.1. Discussion of assumptions and gurantees
OBD pruning은 수학적 기반이 있지만 몇가지 단점이 있습니다.
(1) 완전히 학습된 모델에 대해서 pruning을 수행한다는 가정이 필요합니다. Singh and Alistarh (2020)는 학습이 잘 되지 않은 network (\(\nabla_\mathbf{w}L \neq 0\))에 대해서 OBS를 확장했습니다.
(2) Saliency measure를 계산할 때 inverted Hessian matrix를 사용하는데, 이게 가능한 이유는 pruning을 수행하는 시점에서 해당 point에 대한 Hessian matrix가 invertible 하다는 가정을 했기 떄문입니다. 그리고 pruning perturbation이 작아서 perturbatino 방향으로 Hessian matrix가 상수라는 가정이 필요한데, 왜냐하면 이 가정이 없으면 loss를 근사할 때 hessian matrix보다 더 높은 차수를 사용해야 하기 떄문입니다.
(3) single weight를 제거할 떄 마다 Hessian을 다시 계산해야하기 때문에, 최근에 연구되는 커다란 모델에서는 적용할 수 없습니다. 그리고 Le Cun (1990)이 제시한 방법에서 Hessian matrix가 diagonal이라는 가정하에 pruning 방법을 제시했는데, 이후에 Hassibi and Stork (1992)는 diagonal 가정을 없애고 다른 가정을 추가해서 inverse Hessian을 추정하는 numerical method를 제시했습니다.
3.5.2. Large-scale pruning based on second-order information
Second-order pruning 기법에서 고려해야할 중요한 사항은 large scale network에 대해서 적용이 가능한지 여부입니다. 왜냐하면 파라미터 크기가 클 때 inverse Hessian matrix의 diagonal 성분을 계산하기 어렵고, Hessian matrix가 non-invertible 가능성도 있기 때문입니다. 이런 문제들을 해결하기 위해 OBD를 확장하는 방법들이 연구되었습니다.
The Empirical Fisher Approximation to the Hessian (OBS) 방법은 Hessian matrix를 Empirical Fisher matrix를 이용해서 근사하는 방법인데, Hassibi and Stork (OBS)가 1992년에 가장 처음으로 제시했습니다. 근사할 때 몇가지 가정이 필요한데 softmax를 사용하는 classification task의 경우에만 적용이 가능하고, 학습이 잘 돼서 모델의 output 분포가 true output distribution을 근사한 상태여야 합니다. 두가지 가정하에 Hessian matrix를 다음과 같이 empirical Fisher를 사용해서 근사할 수 있습니다.
\[H \simeq \frac{1}{N} \sum_{j=1}^N \nabla \ell_j \cdot \nabla \ell_j^{\top}\]Approaches based on low-rank inversion 방법은 Sherman Morrison formula를 응용한 방법입니다. Sherman Morrison formula는 어떤 행렬 \(A\)의 inverse를 알고 있을 때, 임의의 column vector \(u, v\)에 대하여 \((A + uv^T)^{-1}\)를 적은 계산비용으로 계산할 수 있는 방법입니다. 이 방법을 응용해서 \(j\)번째 inverse Hessian matrix와 \(j+1\)번째 gradient를 알고있을 때, \(j+1\)번째 inverse Hessian matrix를 다음과 같이 적은 비용으로 근사할 수 있습니다.
\[\widehat{H}_{j+1}^{-1}=\widehat{H}j^{-1}-\frac{\widehat{H}j^{-1} \nabla \ell{j+1} \nabla \ell{j+1}^{\top} \widehat{H}j^{-1}}{N+\nabla \ell{j+1}^{\top} \widehat{H}j^{-1} \nabla \ell{j+1}}\]초기에 \(\hat{H_0}^{-1} = \lambda I_d\) 이고, \(\lambda\)는 작은 값입니다. 이 접근 방법은 OBS에서 small scale에 적용되었는데, 2020년에 Singh and Alistarh가 이 방법을 기반으로 large scale network에 pruning을 적용하는 방법을 제시했습니다. 위의 방법을 사용해서 block-diagonal approximation을 통해 Hessian matrix를 근사했습니다. 이 방법은 unstructured pruning 기준으로 magnitude 방법이나 diagonal Fihser 방법에 비해서 SOTA accuracy를 달성했습니다.
OBD/OBS를 확장하는 방법도 많이 연구되었는데, loss를 기준으로 파라미터의 중요도를 계산하는 게 아니라 generalization error를 기준으로 중요도를 계산하는 방법이 있고, OBS에 weight decay를 추가한 방법, 특정 weight를 제거했을 때 해당 weight와 연관된 모든 weight를 제거하는 방법 등이 있습니다.
3.6. Selection based on regularization of the loss during training
Cost function에 penalty term을 추가하는 regularization을 이용해서 sparsification을 적용하는 방법이 있습니다. Penalty term을 통해 weight가 sparse 형태로 변하고, 모델의 complexity를 낮추게 됩니다. 하지만 penalty term을 추가하면 local minima가 추가적으로 생겨서 최적화된 파라미터 값을 찾기가 더 어려워집니다.
3.6.1 \(L_0\) norm
Sparse weight를 생성하는 가장 명확한 방법은 weight의 \(L_0\) norm을 penalty term으로 사용하는 것입니다.
\[P(\mathbf{w})=\alpha\|\mathbf{w}\|_0=\alpha \sum_j \begin{cases}0 & w_i=0 \\ 1 & w_i \neq 0\end{cases}\]\(L_0\) norm은 파라미터 안에 0이 아닌 원소의 개수를 세는 metric인데, discrete한 특성 때문에 미분이 불가능해서 직접적으로 최적화하기가 어렵습니다. 이 문제를 해결하는 가장 단순한 방법은 Straight-through estimators (Bengio, 2013)을 사용해서 backpropagation 과정에서 미분이 불가능한 point를 identity function으로 대체하는 방법입니다. 몇몇 사람들은 이 방법이 불안정하다고 해서 Softplus 혹은 Leaky ReLU를 사용해서 미분 불가능한 point를 근사했습니다.
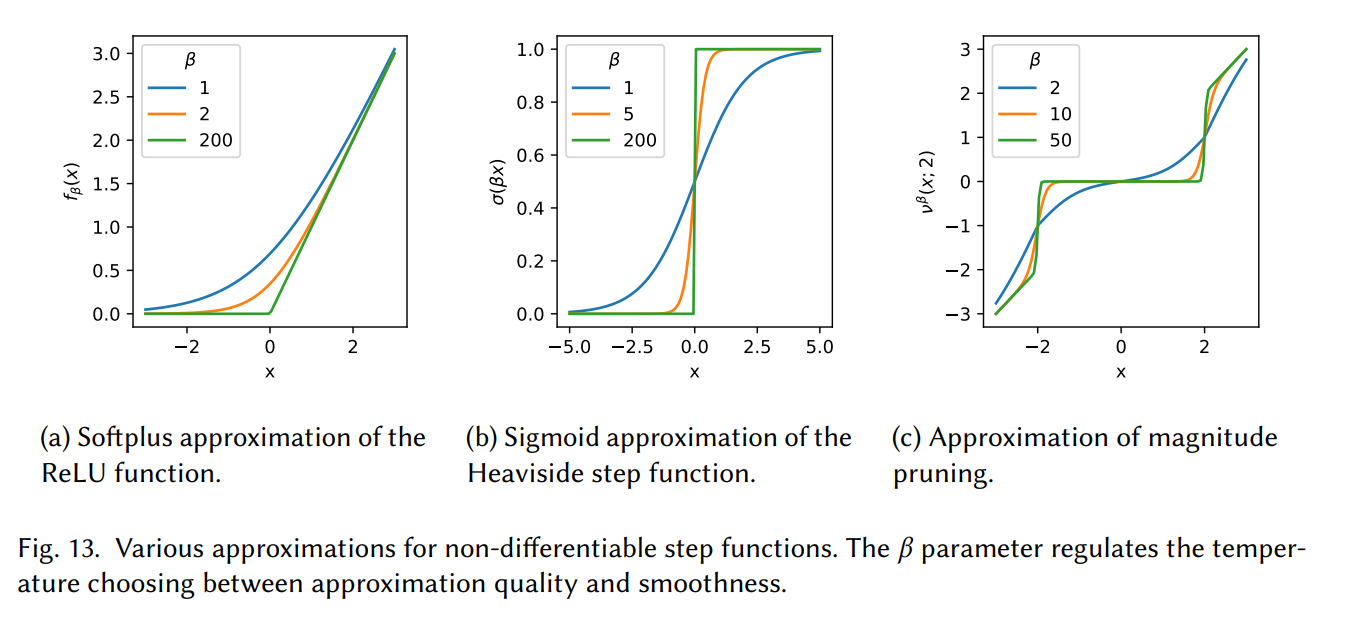
미분 불가능한 point를 근사하는 두번째 방법으로는 parameterizable continuous function을 사용하는 것입니다. Luo and Wu (2019)는 sigmoid function을 사용해서 Heaviside step function을 근사했습니다. 그림 13 (b)에서 \(\beta\)값이 커지면 step function에 가까워지지만 학습하기가 어려워집니다.
마지막으로 magnitude pruning 할 때 threshold를 직접 학습하는 방법이 있습니다. Manessi (2018)는 threshold linear function을 다음과 같이 정의했습니다.
\[v^\beta(x, t)=\operatorname{ReLU}(x-t)+t \sigma(\beta(x-t))-\operatorname{ReLU}(-x-t)-t \sigma(\beta(-x-t))\]여기서 \(t\)는 threshold parameter이고 \(\beta\)를 조절해서 threshold 바깥에 있는 point의 기울기의 sharpness를 결정합니다. \(t\)안에 있는 입력은 0에 가깝게 만들고, \(t\) 바깥에 있는 값은 선형함수에 가깝게 근사하는 방법입니다.
\(L_0\) norm 과 관련있는 다른 pruning 방법으로는 Polarization (Zhuang et al., 2020)이 있는데, 이 방법은 다음과 같은 regularizer를 사용해서 파라미터에서 몇개의 element는 0에 가깝게 만들고, 다른 element는 0에서 멀어지게 만드는 방법입니다.
\[R(\alpha)=t\|\alpha\|_1-\left\|\alpha-\bar{\alpha} 1_n\right\|_1=\sum_{i=1}^n t|\alpha_i|-|\alpha_i-\hat{\alpha}|\]여기서 \(\bar{\alpha}=\frac{1}{n} \sum_{i=1}^n \alpha_i\)인데, \(\left\|\alpha-\bar{\alpha} \mathbf{1}_n\right\|_1\) 이 값은 \(\alpha_i\)가 모두 동일할 때 최대가 되고, 절반이 0이고 나머지 절반 값이 같을 때 최대가 됩니다. 이런 성질로 인해서 값이 큰 weight과 작은 weight을 분리시켜주는 역할을 합니다.
3.6.2. \(L_1\) norm
Lasso라고도 알려진 \(L_1\) norm은 \(L_0\) norm의 tightest convex relaxation 형태입니다. \(L_0\) norm과는 다르게 penaty function이 선형이어서 미분이 가능합니다.
\[P(\mathbf{w})=\alpha\|\mathbf{w}\|_1=\alpha \sum_i\left|w_i\right|\]\(L_1\) penatly는 직접적으로 weight를 0으로 만들지 않고 값을 작게 만들기 때문에 magnitude-based 방법과 같이 사용이 됩니다. \(L_1\) 기반 방법의 단점은 \(L_1\) norm이 scale에 variant하기 때문에, 모든 파라미터를 같은 속도로 감소시킨다는 것입니다. 이러한 이유로 \(L_1\) norm이 효율적인 sparsity 방법이 아니어서 Yang (2020)은 Hoyer regularizer를 사용해서 \(L_1\) norm의 단점을 보완하는 방법을 제시했습니다.
\[H_S(\mathbf{w})=\frac{\left(\sum_i\left|w_i\right|\right)^2}{\sum_i w_i^2}\]Hoyer regularizer는 \(L_1\) norm과 \(L_2\) norm의 비율로 구성돼서 scale-invariant한 penalty term 역할을 합니다. 논문에서는 Hoyer regularizer를 사용해서 같은 accuracy를 기준으로 sparsity가 더 큰 모델을 만들었습니다.
3.6.3. Grouped Regularization
Group lasso는 같은 group안에 있는 변수들을 모두 0으로 혹은 0이 아닌 값으로 만드는 방법입니다. \(N\)개의 element를 \(G\)개의 그룹으로 나누고 \(X_g\)가 각 group의 원소를 포함하고 있다면, group lasso는 다음과 같은 최적화 문제를 푸는 형태로 정의가 됩니다.
\[\min_{\beta \in \mathbb{R}^p}\left(\left\|\mathbf{y}-\sum_{g=1}^G \mathbf{X}_{\mathrm{g}} \beta_g\right\|_2^2+\lambda \sum_{g=1}^G \sqrt{n_g}\left\|\beta_g\right\|_2\right)\]그룹은 보통 특정 뉴런과 연결된 모든 output으로 설정하거나, CNN의 경우는 필터 혹은 채널, 아니면 전체 layer에 대해서 설정할 수도 있습니다.
3.7. Variational selection schemes
Pruning을 적용할 뉴런을 선택하는 다른 방법에는 Bayesian 접근 방식이 있습니다. 여기서는 만약에 특정 뉴런의 variance가 크다면 네트워크 성능에 기여하는 부분이 적다고 가정하고 해당 뉴런을 제거하는 방식입니다. 대표적인 예시로 Sparse Variational Dropout (Sparse VD) (Molchanov, 2017) 방법이 있는데, 이 방법은 각 weight를 정규분포 형태로 parameterization 해서 학습하는 동안 해당 파라미터를 학습합니다.
\(\mathbf{w} \sim \mathcal{N}\left(\mathbf{w} \mid \theta, \alpha \cdot \theta^2\right)\)라고 한다면 \((\theta, \alpha)\)를 학습하는데, 여기서 \(\alpha\) 값이 크다면 test할 때 해당 뉴런을 0으로 설정해주는 방식입니다. 직관적으로 보면 \(\alpha\)가 크다는건 해당 뉴런에 noise가 많아서 network의 performance에 나쁜 영향을 준다는 것입니다. 이 방법의 장점은 추가적인 hyperparameter tuning 과정이 필요없고, 방법이 비교적 단순하다는 점입니다.하지만 각 weight당 2개의 파라미터가 있기 때문에, 모델 사이즈가 2배로 커진다는 단점이 있고, 아예 처음부터 Sparse VD로 학습하는게 어려워서, pre-trained model에 적용을 하거나 다른 추가적인 기법을 사용해서 학습을 보완해야 합니다.
Sparse VD 방법을 통해 sparse neural network를 만들었지만, unstructured 형태로 pruning이 진행되기 때문에 inference 속도에는 거의 변화가 없습니다. 그래서 structured 형태로 variational dropout을 적용하는 Struc-tured Bayesian pruning 기법이 있습니다. Neklyudov (2017)은 각 파라미터를 log-normal distribution 형태로 표현하고, 각 group마다 variational parameter를 공유하는 형태로 모델을 설계했습니다. log-normal noise는 항상 non-negative 여서 입력의 부호를 바꾸지 않고, closed-form 형태로 variational lower bound를 표현할 수 있다는 장점이 있습니다. 뉴런을 제거할 때는 뉴런마다 signal-to-noise ratio (SNR)을 계산해서 SNR이 낮은 그룹을 제거했습니다. 이 방법은 CIFAR-10 이나 MNIST같은 작은 데이터셋에 대해서 가속이 잘 되었습니다.
Comments powered by Disqus.